I've been assembling a printer from some of the parts of a Prusa i3 Mk2.5, but using a Mini5 as the control board.

The inductive sensor I have is a (completely genuine bought from Prusa) 'pinda' V2, which is acknowledged to have some temperature dependence, but has a built-in thermistor to permit corrections. I didn't trust the Pinda V1 at varying temperatures, and have always done all bed preheat with the printhead as far from the bed as possible to minimise heat effects.

I should acknowledge https://forum.duet3d.com/post/302443 which specifies some thermistor parameters (100k, B=3950) and a temperature coefficient (0.02) because (spoiler!) although I now think the parameters for mine are very different from that, it was a useful part of getting to this point.

With RRF it should be relatively easy to confirm calibration, because you can probe, heat up the probe by heating the bed (my printer is in an enclosure, so this is fairly effective), then probe again and see what happens. Indeed, the stock Prusa had a function to calibrate something like this - sitting the head just above the bed for a few minutes while it heated and periodically probing. However, it turns out to not be that straightforward.

My first pass did exactly that - put the nozzle just above the bed, switch the bed on, probe every time the pinda gets half a degree hotter than it was and see what happens. I got this:

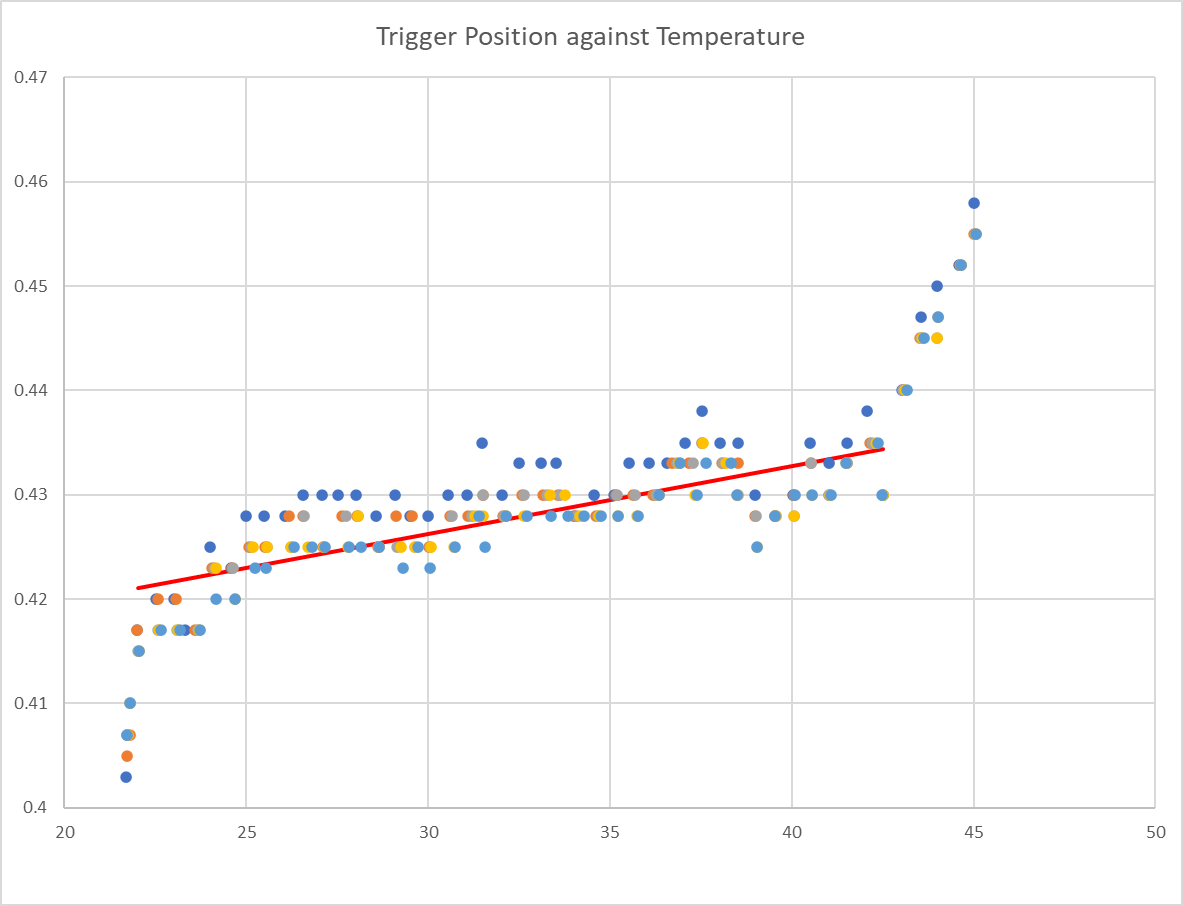
Interesting observations are linearity-ish through the middle, but it's much lower coefficient than the post referenced above (in this case about 0.001 - one twentieth) and the non-linearity at beginning and end. After a number of runs of this I noticed something and when I return to that first data set it's there to see too. This is the graph of temperature against time for that run:

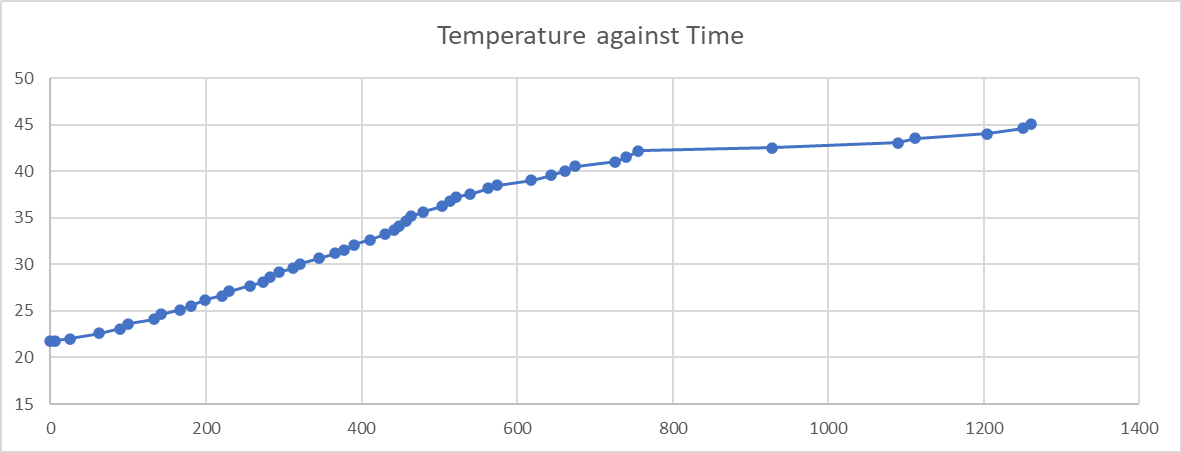
So that dramatic change in apparent temperature coefficient from about 42 degrees correlates with a dramatic change in time it takes to get to each temperature increment. This leads me to think that the thermistor in the probe heats up faster than the electronics - so when the temperature is rising (fairly) quickly, the electronics are actually cooler than reported and so exhibit less apparent temperature dependence.

So then I did it again. This time I coded a more complex heating algorithm - it uses PID (but not very tuned) to adjust the bed setpoint temperature as if it was the power input and tries to hold the pinda at a constant temperature for 40 minutes before taking four sets of probe readings at 5 minute intervals, with 3 probes per set and then moving on to the next temperature.

This does of course come with the caveat that I’m assuming my bed doesn’t itself move at different temperatures. I suppose I could set up a dial gauge on it (but the only one I have has lost its spring, so not terribly useful).

This is fairly successful (with some cheating on the first cycle to avoid a massive over-temperature spike while the integral term initialises / stabilises) and I typically get a temperature v. time from the pinda thermistor like this (red dots are where probing was done):

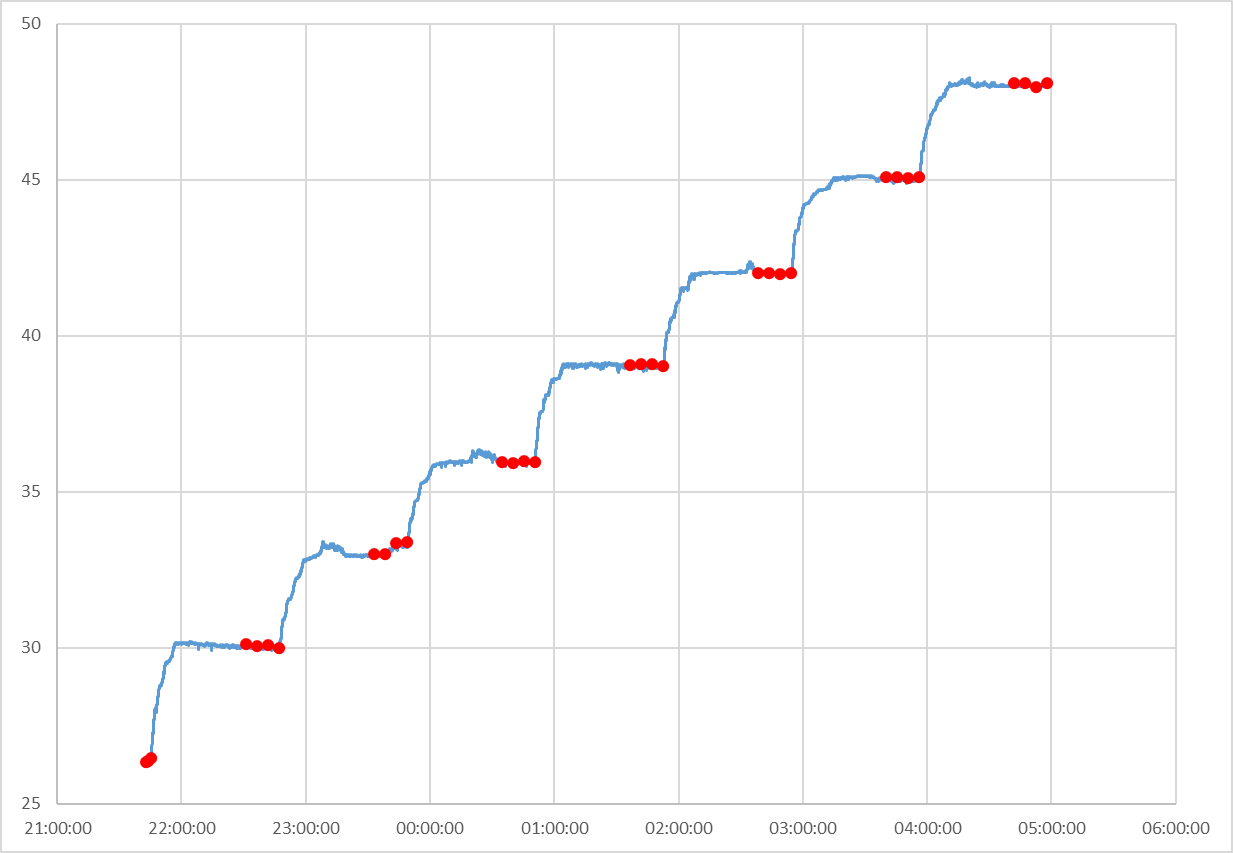
Now I get a more consistent temperature coefficient, which is distinctly non-linear, but which matches quite nicely to a 2nd order polynomial that RRF can accommodate.

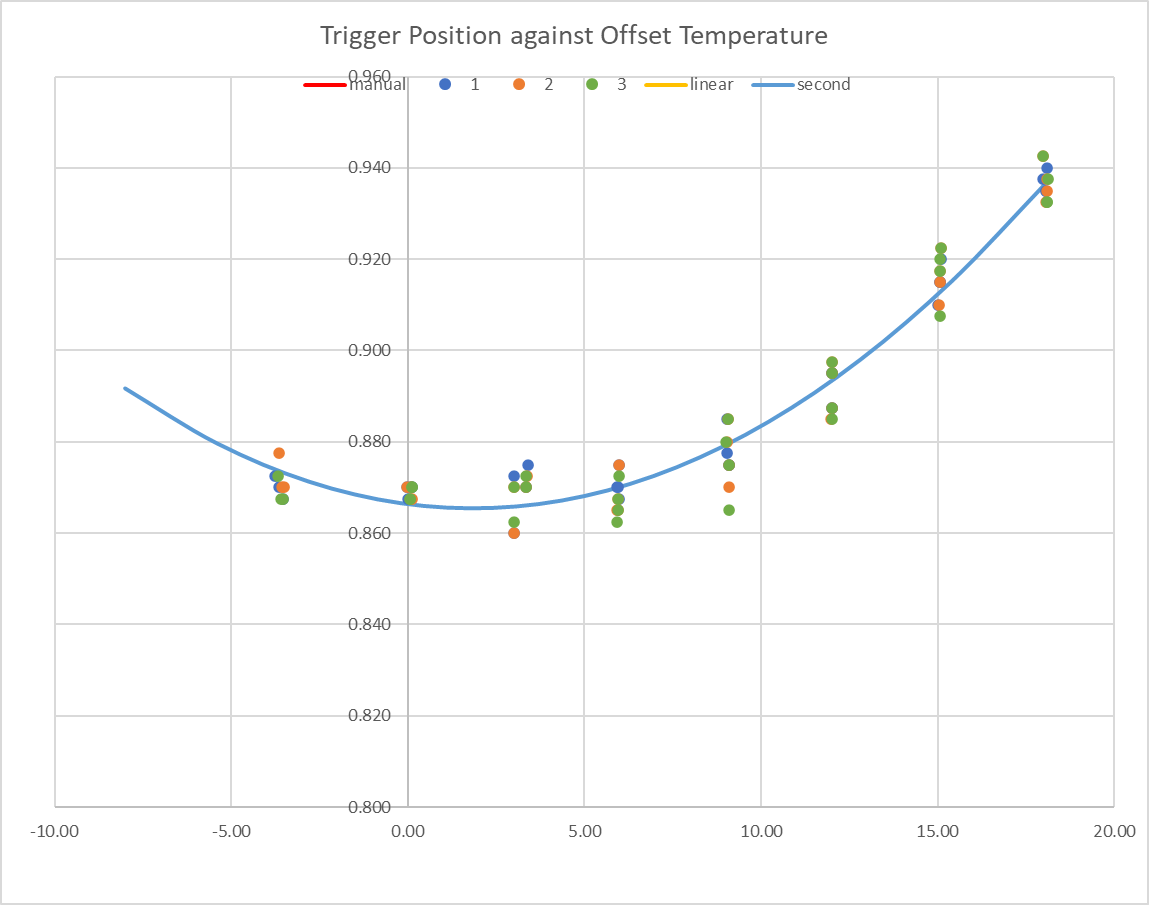
The first readings (before the bed is heating at all) are often off the curve, but by varying degrees. I haven't come up with any good hypothesis for this. This is another run, with an unusually large first set difference.

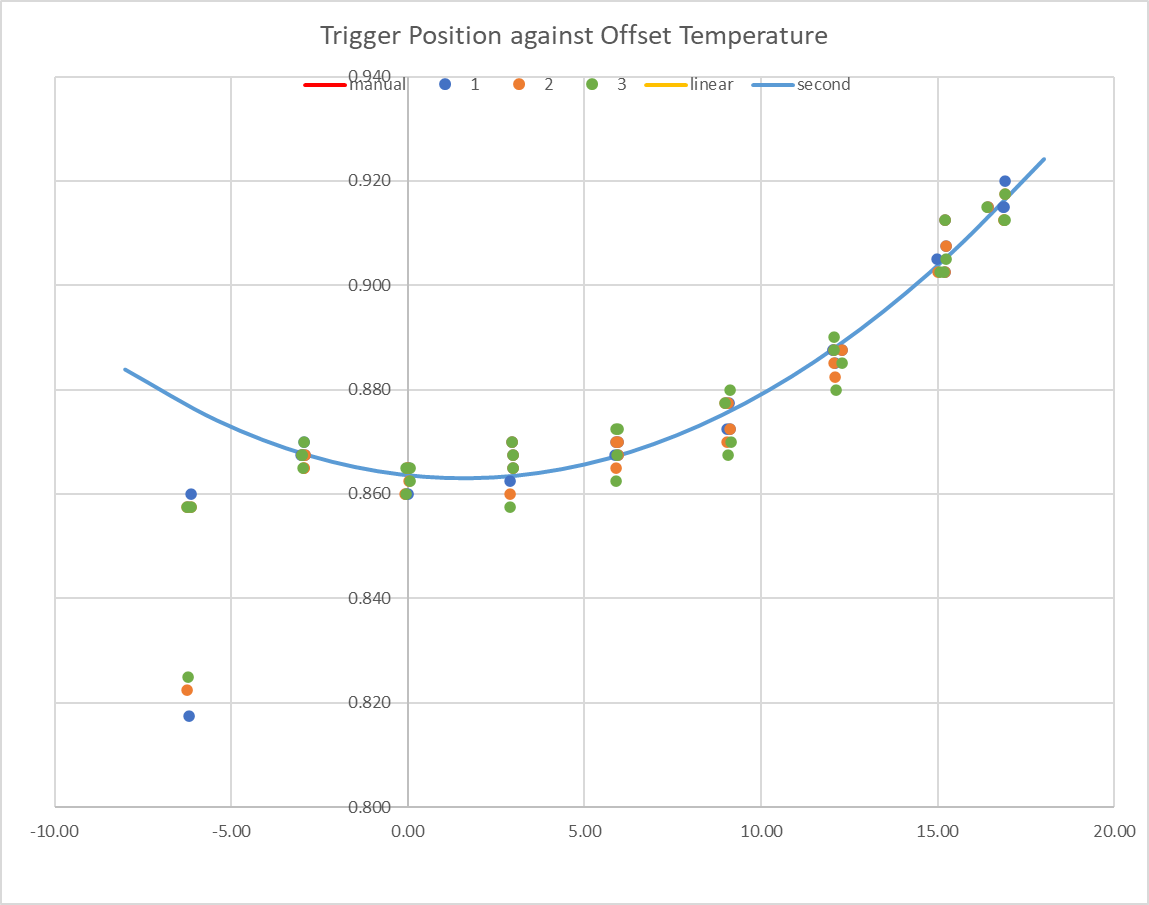
If I neglect the pre-heating data and put multiple runs on one graph, I find that the behaviour is relatively consistent. I first discovered my homez approach was not giving me a consistent result, which manifests as all the points in the test-run matching the curve relative to each other, but offset by an absolute amount up up to 0.06mm low (i.e., the homez has apparently set up the axes too high). I’ve changed my homez to do multiple head movements much slower, and that seems to have fixed the issue.

Also, I’ve set zero compensation for the duration of this testing, so actually the homez is setting to 0.87mm regardless of probe temperature at the time, which will introduce the error I’m trying to quantify into my testing.

For both these reasons, I take the data from a single test run (typically 32 G31s in eight sets of four readings at each temperature), fit a second order polynomial, find the shift that would bring the polynomial to my calibration value (0.87mm at 30C), then apply that shift to all the data in that test. When I do this, the resulting scatter across all the tests (five runs and counting) is about the same as the scatter within any one test.

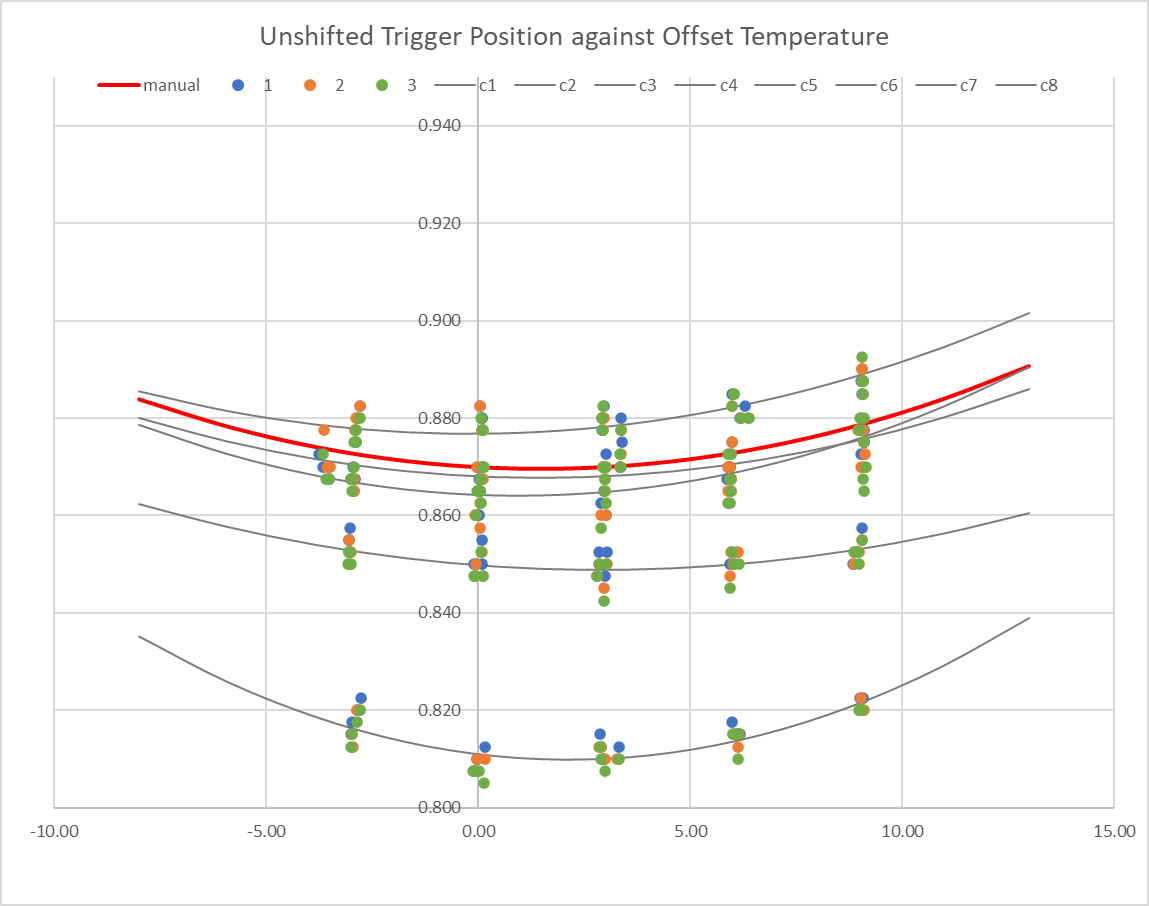
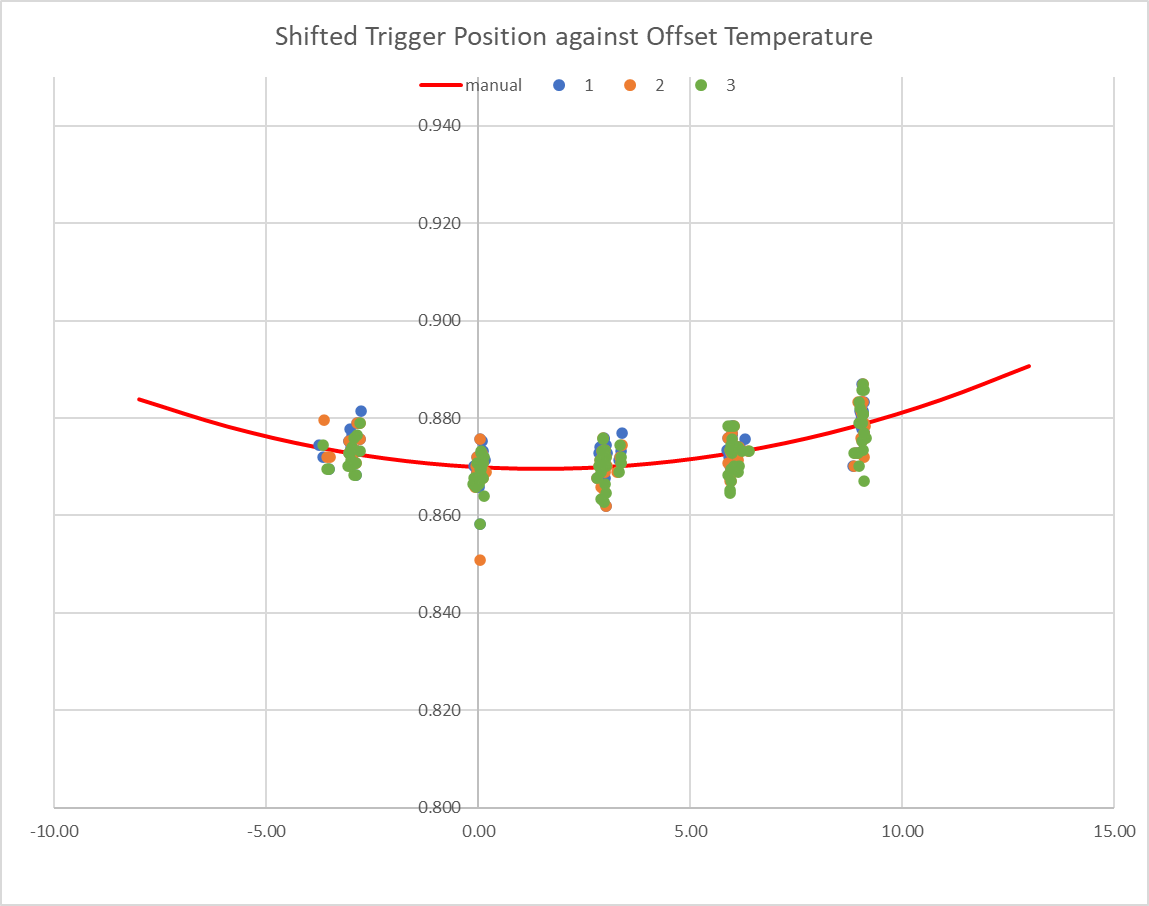
I'm curious how the Prusa firmware manages to do a calibrate in a few minutes if this time dependency exists, but possibly it doesn't actually calibrate directly, and just takes some readings that it uses to adjust the built-in calibration.

This is fairly niche information, I appreciate, but I thought I'd post in case anyone is interested. Actually, my main conclusion is that I didn’t really need to bother, because my conclusion here is that over a 15C range where I’m interested (most of my prints start with the probe at about the same temperature), the trigger height only varies by 0.01mm (ish).

From reading on (mainly Prusa) forums, I suspect that Pinda v2 probes are possibly not only temperature-dependent but also show quite widely varying dependence – there are a number of reports of people changing probe and suddenly finding calibrating the first layer much easier or much more difficult. Possibly I’m lucky with a low-variation one.

Even without such a (hypothesised) variation, this specific data may not be relevant to anyone else, because the apparent temperature correlation is a function of the thermistor properties (I have no idea how consistent the thermistor is), the electronics actual dependency and the behaviour of the bed (i.e., my bed likely moves differently in response to temperature than anyone else's - it's initially a Prusa heated bed, but I've modified it a bit and it's not on a Prusa frame).

Conclusion

So the conclusion to all that is that I've got a calibrated 2nd order polynomial temperature compensation, but actually it's a small enough effect that I could do without. I'm using T-0.000470:0.000159 in my G31 config settings, which over the range 25 to 35C (where I normally am when probing the bed at the start of a print) that equates to a variation in trigger height of only 0.007mm (between max and min), or about three microsteps.

Workings

The rest of this is what I used to conclude the above

This is my macros that do the calibration (you need both because probeTcalib calls probe3), note that there are configuration variables in the start of both that need setting (e.g. which sensor is the one in the pinda). As noted, I set a zero temperature coefficient for the probe before running this, but I think the lastStopHeight is reported without temperature compensation (i.e. the compensation is not applied to the stop height, it's applied to the probe offset value used to set the head coordinates) so that wouldn't actually matter.
probeTcalib.g
probe3.g

This is the spreadsheet that I use to analyse a single run, but I've taken out the 32000+ rows of temperature values to shrink the file size. If anyone wants my data I'm happy to email an example - the spreadsheet with the temperature log data is about 3.5MB.
probe T calibration - 20230304 - pruned.xlsx

This is the spreadsheet with multiple runs overlaid. The first two cases in this are with my ‘inaccurate’ homez , resulting in a ‘large’ shift (up to 0.06mm) the others are with my new homez and shift is about a tenth of that. (For information, my Z axis is 400 steps/mm, or 0.0025mm per step).
probe T calibration - combined limited.xlsx

I think there is maybe one other person on the planet using my filament weighing plugin (https://forum.duet3d.com/post/253602), but notwithstanding that, this updates it for firmware 3.5.1 and a fresh Bookworm DuetPi. There's also some tidying up internally.

This is the plugin file (but you will need to take the .txt off the end of this file - I'm circumventing the forum restrictions): WeighFilament.zip.txt

WARNING

This one is not as good as the old one on 3.4, because I can't get http endpoints to work on 3.5.1, so I can't put a continuously updating display on the DWC screen. However, this one sets up a global variable with the weight value in it, so you can define a macro containing e.g. M291 P{global.filWeight^"g filament on spool"} R"Filament Weight" and get the weight at the click of a button, so it's useful.

I do intend to revert to the old functionality when I can figure it out. The problem might be that I'm jumping the gun - I'm using pre-release dsf-python-3.5.0.2rc2 with 3.5.1 RRF and DWC, and that's not a combination that's listed as compatible at https://github.com/Duet3D/dsf-python/releases.

For now, this plugin is purely DSF, no DWC component at all.

What it does

It connects a HX711 load cell amplifier direct to a Pi so you can build a load-cell into the spool holder and have a report of filament weight on the spool. The weight of filament is written into a global variable (global.filWeight, but that's configurable) for you to do whatever with.

A python3 DSF routine takes one new weight reading every three seconds (configurable), and averages over the previous 12 readings (configurable). It uses a simple IQR-based filter to disregard outliers in the data, which should eliminate the odd faulty readings. It tries to spot step-changes (e.g. lifting the spool off the holder) and if it does, it reads a whole new set of 12 readings at once, so you get a quicker update of weight (around ten seconds) and it should jump straight from previous weight to new weight without sliiiiding from one value to the next. The global variable is only updated if the weight is more than 5g different to what it last reported (threshold is configurable). The aggressiveness of the IQR filter is configurable too.

There are obvious (and explained) values in the start of /opt/dsf/plugins/WeighFilament/dsf/weighfilament.py you can change to modify all the configurable items.

There is a helper script that records tare weights and calibration values.

Hardware

Hardware is a HX711 breakout and single-point load cell. Mine is an ebay-cheap-special 3kg cell, 13x13x80, and the cheapest available green breakout. The load cell plus board is probably only £5 on ebay. Connect loadcell wires to the breakout (loads of instructions on probable colour scheme the web) and then breakout to a 3.3V pin, a 0V pin and two GPIOs on the Pi - the code assumes DAT to GPIO5 and CLK to GPIO6 (configurable). Note that the HX711 has two hardware channels - channel A can do either 128x or 64x gain and B can do 32x gain - you need to connect the cell to the correct channel for the gain you are using.

Installation and Calibration

You need some python libraries. At a command prompt: sudo apt install python3-numpy. The previously required python3-rpi.gpio and python3-setuptools seem to already be part of the latest DuetPi image.

You need to download and install the dsf-python from https://github.com/Duet3D/dsf-python/releases. As noted above, I'm currently using dsf-python-3.5.0.2rc2 which is pre-release. I haven't tested other versions. Having downloaded and unpacked you cd into the library top folder and sudo python3 setup.py install.

You need to download and install the HX711 library from https://github.com/tatobari/hx711py This is pure python and relatively straightforward. Having downloaded and unpacked you cd into the library top folder and sudo python3 setup.py install. Note that the author has done some (relatively) recent changes to the library - I'm not using the new functionality, which is mainly focussed at increasing the speed of reading - the old functionality works fast enough for this use case.

To install the plugin drop the zip onto the 'Install Plugin' button in Plugins / external plugins in DWC - but DO NOT START the plugin yet.

The plugin won't create the necessary global variable, only update an existing one, so you need to add creation of the variable to config.g, e.g. with the following. The value you set here doesn't matter. You can use a different variable name, but in that case must edit the value near the start of /opt/dsf/plugins/WeighFilament/dsf/weighfilament.py to match.

if !exists(global.filWeight)
    global filWeight = 0

You need to calibrate the routine before use. The plugin has a helper script to do that, and it's easiest to put this into /usr/local/bin so you can run it directly. At a command prompt run sudo cp /opt/dsf/plugins/WeighFilament/dsf/weigh /usr/local/bin and then sudo chmod a+rx /usr/local/bin/weigh.

With nothing on the spool holder at a command prompt run weigh zero, this records the tare reading of the holder alone.

Then you need something of a known weight not dissimilar to a spool of filament (preferably nearing the end) on the holder - I use a 200g weight - and run weigh calib. It will ask you what the weight is.

Then preferably put an empty spool on the holder and run weigh spool. If you don't have an empty spool but do know what one weighs you can run weigh manual and enter a weight value.

Actually, you can abbreviate the weigh options to the first letter, and scatter '-' around too - instead of weigh zero you can weigh z or weigh -z or weigh --zero or weigh zipadeedoodah etc.

Some semi-cryptic entries should now have shown up in the weighfilament_calib.txt file in the system directory.

You can re-run any of these (e.g. when you change to a spool with a different empty weight), but you must stop the plugin first. There is no locking, and the script and plugin will scramble each other's communication with the HX711 if they run simultaneously, normally resulting in a hang or garbled data. The calibration file grows forever, if you do a lot of resetting the calibration you can open it and delete older lines - the routine just uses the last of each 'zero', 'calib' and either 'spool' or 'spoolwt' lines it finds in the file.

If you get wildly varying (or complete garbage) answers or the script hangs, the plugin is probably running. Stop the plugin before running the script. Also, the plugin only reads the calibration file on startup - so you need to start the plugin after changing calibration values for it to get the new values anyway.

However, there is apparently the possibility of problems with bit ordering and byte ordering which can also lead to garbage values - if you still get garbage values see the discussion on the HX711 library github page and make changes in definitions near the top of both the helper script and the weighfilament.py file in the plugin zip file.

After all that you should be able to start the plugin. Apart from 'Status' changing to 'started' nothing visible will happen, but if you look in the object model browser or run M291 P{global.filWeight} you should get a weight. I have a macro as defined near the top of this posting to prettify it a bit.

So I put my 3D printer bed back together, complete with tidy covers around the print bed, and found a slight hardware bug remarkable feature:

I can do a remote hard power-off:

G1 X0 Y140 Z0.5
G1 X-50

does this: https://player.vimeo.com/video/487182136

In what is undoubtedly the biggest sofware release of the day I have implemented another filament weighing plugin for a system with an attached Pi.

Actually, half of it is a direct lift of Resam's plugin described at https://forum.duet3d.com/post/241194. I have taken the DWC plugin from that but written a new python DSF routine. Mine is for a HX711 directly connected to the Pi. Resam reports getting noisy / faulty readings with an HX711 connected directly, but I get very few - this may be subject to all sorts of vagaries of wiring etc.

My DSF routine uses a simple IQR-based filter to disregard outliers in the data, which should eliminate what faulty readings do occur. It takes one new reading every three seconds, and averages over the previous 12 readings. It tries to spot step-changes (e.g. lifting the spool off the holder) and if it does, it reads a whole new set of 12 readings at once, so you get a quicker update of weight (around ten seconds) and it should jump straight from previous weight to new weight without sliiiiding from one value to the next.

I also have a helper script that records tare weights and calibration values.

Hardware is a HX711 breakout and single-point load cell. Mine is an ebay-cheap-special 3kg cell, 13x13x80, and the cheapest available green breakout. Connect cell wires to the breakout (loads of instructions on probable colour scheme the web) and then breakout to a 3.3V pin, a 0V pin and two GPIOs on the Pi - the code assumes DAT to GPIO5 and CLK to GPIO6 (but there are parameters in the top of the .py file in the zip if you want to pick different ones). I created a spool holder in OpenSCAD, and because my printer is a delta the spool axis is at 30 degrees. Also beware, this holder is only 80mm wide (between upstands).

weigh_spool.scad

How it works:

The plugin creates an endpoint on the printer at http:<machine name or IP address>/machine/filament-load-cell/reading. The endpoint shows the latest measured filament weight (or a comment about why not). The DWC plugin periodically grabs the text from that endpoint and inserts it into the banner of the DWC page. In this version, the code of the endpoint is by me, the code that sticks the text into the DWC page is by Resam.

The plugin is here (but you'll need to remove the .txt - that's me circumventing the forum system): WeighFilament.zip.txt

I strongly suggest unzipping it and reading through before installing so you know I'm not doing something nefarious with your printer.

The helper script is here: weigh.txt (again, you probably want to rename it without the .txt)

Note that I don't consider myself much better than 'can make myself understood' in python, and I despise it, and my coding is not 'pythonic'. Feel free to improve it. It's MIT licence. I don't mind what you do with it, I don't warrant it fit for anything, if it breaks anything you get to keep the pieces.

Installation:

You need some python libraries: sudo apt install python3-rpi.gpio python3-numpy python3-setuptools (others too, but they are probably already installed).

You need to download and install the HX711 library from https://github.com/tatobari/hx711py This is pure python and relatively straightforward. It appears to be written for python2, but runs happily under python3 as well, so having downloaded and unpacked you cd into the repository folder and python3 setup.py install.

Enable the plugin service on the Pi. See https://forum.duet3d.com/post/219064 (but that says you won't need to do that soon). (Also, I don't think I put apparmor in my cmdline.txt, and it seems to work for me).

The helper needs to write to a state file somewhere. sudo touch /var/lib/misc/spoolweigh.txt and sudo chmod 666 /var/lib/misc/spoolweigh.txt. You can put it elsewhere but you'll need to edit both the helper script and the weigh_filament_endpoint.py file in the plugin zip file. This file will grow every time you calibrate or use a different weight spool. You can just prune older lines - the plugin uses the last relevant content it finds - it needs a 'zero' line, a 'calib' line and either a 'spool' or a 'spoolwt' line.

Do the initial calibration before running the plugin. This is all by the command line on the Pi, so you need a command terminal / window / whatever. Put the helper script somewhere, make it executable, and then you can run it. First, with nothing on the spool holder run weigh zero, this records the tare reading of the holder alone. Then you need something of a known weight not dissimilar to a spool of filament (preferably nearing the end) - I use a 200g weight - and run weigh calibrate. It will ask you what the weight is. Finally, preferably put an empty spool on the holder and run weigh spool. If you don't have an empty spool but do know what one weighs you can run weigh manual and enter a weight value. You can re-run any of these (e.g. when you change to a spool with a different empty weight), but you must stop the plugin first. There is no locking (for various reasons, not least my lack of competence), and the script and plugin will scramble each other's communication with the HX711 if they run simultaneously, normally resulting in a hang or garbled data.

Actually, you can abbreviate the options to the first letter, and scatter '-' around too - instead of weigh zero you can weigh z or weigh -z or weigh --zero or weigh zipadeedoodah etc.

If you get garbage answers or the script hangs, the plugin is probably running. Stop the plugin before running the script. (Also, the plugin only reads the file on startup - so you need to start the plugin after changing calibration values for it to get the new values anyway). Stop the plugin before running the script.

However, there is apparently the possibility of problems with bit ordering and byte ordering which can also lead to garbage values - if you get garbage values see the discussion on the HX711 library github page and make changes in definitions near the top of the helper script and the weigh_filament_endpoint.py file in the plugin zip file.

The helper also does weigh filament to report the weight of filament on a spool on the holder, weigh gross to tell you the weight of everything on the holder (i.e. typically spool plus filament), weigh quick / weigh quiet which does fewer readings and does less chit-chat, weigh raw which gives you the rawish data coming back from the HX711 and does no outlier filtering or conversion to weight units. Probably use these to check it's behaving itself before using the plugin.

Once the zero, calibrate and spool are done, you can install the plugin by dropping the .zip file onto the 'UPLOAD & START' button in DWC. If I haven't forgotten a critical step above, the weight of filament on your spool should appear alongside the machine name (here it is on my imaginatively named delta printer):

It reports to the nearest 0.1g, but don't confuse resolution with accuracy. I find the reported weight wanders around by about 2 or 3g day-to-day. Also, note that unless your filament exits the spool horizontally, the vertical component of pull force on the filament contributes (positive or negative) to the weight reading whenever the printer is extruding.

Back in early 2020 I started building a new 3D printer (I already had a Prusa Mk2) and I've just finished all the things I had in mind when I started, so while I hesitate to say it's finished, here it is.

In essence it's a fairly standard delta, though built with genuine brand components from the 'good' end of the range, so it's Duet MB6HC plus smart effector (I ordered that just before the mini 5+ was announced!), Hiwin rails, Gates 9mm belts, Haydn Huntley carbon rods, Bondtech BMG, Meanwell PSUs, E3D V6 (copper block, titanium heatbreak), magnetic bed. Suppliers are from among the usual suspects (RobotDigg, Ooznest, E3D, Farnell, Digikey) plus www.lasermaster.co.uk (no relationship other than happy customer) who did all the aluminium laser cutting - I've used them for mild steel, stainless and aluminium in all sorts of sizes and thicknesses (including some very small orders) and always been happy.

PSUs are in base, along with SSR for the mains heated bed. I have a 350W 24V and a 200W 12V - the latter drives a 5A POL DC-DC convertor at the Raspberry Pi to generate 5V for the Pi, the Duet board and the LEDs. The 24V PSU is powered via a real relay (I don't like putting PSUs on SSRs - but that's just a superstition of mine). Both PSUs are fanless, but the bottom aluminium plate is deliberately chunky (as a heatsink) and there's an arduino (actually a teensy) with thermistors on each of the PSUs which runs a fan if required. There's a spare SSR in case I heat the enclosure in future.

Duet, Pi, steppers and a vent for the enclosure are in the top. The top enclosure has a single cooling fan blowing air in direct onto the stepper drivers, and a small centrifugal fan blowing air across the underside of the MB6HC. I thought the Pi might want a fan, but it hasn't - there's a largish heatsink on the processor, but it doesn't get much above 55C. My wiring will probably give the voron crowd conniptions, but I'm working on the basis that parallel wires risk cross-talk (honest).

The vent for the enclosure has some servo-driven blades. Daemon.g opens and closes it just below the temperature when the fan cuts in.

There's a spool holder with built-in weighing load cell so I get a report of how much filament remains - I've posted about that recently at https://forum.duet3d.com/topic/25419/another-weighing-filament-holder

There are two rows of LEDs (actually, one row of 40x SK9822 and a row of 12x APA102, and they are joined end-to-end as one string) to provide status information from across the room. One row gives me a progress bar (showing heater 0 and 1 when they are heating and file progress when the heaters are at temperature) and the other row gives me status of heaters, fans and power. Heater lights slide from blue if the heater is more than a few degrees below set-point through green at set-point to red if it's more than a few degrees above set-point. Fan lights are just on green if the fan is on (but I can set them to show varying colour with PWM duty). The power lights likewise change colour if the voltage deviates by more than 0.5V from where it's supposed to be.

Heater progress bars grow form each side to meet in the middle, so this tells me the nozzle is about a third of the way to temperature and the bed is two-thirds. Reading across the second row I see that two heaters are cold (blue), one is OK (the enclosure is always OK if it's not too hot), there's one fan on, the 24V is good and the system is on:

File progress is just one left-to-right bar, so here it is having barely started on a file (actually about 3.5% - green is a 'full' slot and blue is a fractional, sliding from dim dark blue through bright cyan to green), and here nozzle and bed heaters are OK, the enclosure is hotter than it should be, three fans are running (print cooling, hot end, electronics enclosure), the 24V is good and the system is on:

The lights script is set up as a systemd service, so runs automatically on boot.

If I'm not across the other side of the room, there's also a PanelDue 5i, as you can see.

The enclosure is illuminated by white LEDs down the back side of the left and right legs (so flood the interior when on), but it doesn't really need them. They are just switched by the rocker switch you can see near the LEDs. The front door is on a magnetic catch and opens to 120 degrees, but can also just lift off the hinges.

This is a Duet Software Framework (DSF) plugin that duplicates similar behaviour to 'daemon.g', except that it runs python code (python 3) on an attached Raspberry Pi when the printer is running SBC mode. The python code has access to a recently-updated copy of the machine object model, and can set the interval to the next time the code runs.

A python3 DSF routine runs every 'loop interval' seconds, looks for a specified file in a specified location (by default daemon.py in the printer sys folder, which is at /opt/dsf/sd/sys/ on the Pi - these can be changed but note that the filename must end in '.py'). If the file exists, it runs the function 'loop()' (if it exists) from within that file each interval. If the file has changed (or appeared) since the last check, the function 'setup()' (if it exists) from the file is run first immediately before running loop().

That is, the daemon.py file functions are somewhat like the functions in an arduino sketch - setup() is run once, and then loop() is run repeatedly. However, in this case, loop() is run only periodically, as defined by the 'loop interval'.

Note that the functions run 'on the dot', so if the interval is set to 60 (i.e. 60 seconds, i.e. 1 minute) loop() runs every minute on the minute, whether the function takes milliseconds to complete, or 59 seconds to complete. However, it runs on the next occurrence of the time interval, so if the interval is set to three seconds, but the function takes four seconds to run, it will actually be run every six seconds: starts at ...0, finishes at ...4, the next multiple of three is ...6 so it runs then and finishes at ..10, the next multiple is ..12 so it runs then and finishes at ..16 and runs again at ..18, etc.

Both functions are called with a dict-of-dicts-of-... parameter that contains the entire object model at the current time (though it can be up to about 2 seconds out-of-date). Thus, within the python functions, object model elements can be accessed with e.g. print(object_model['heat']['heaters'][1]['active']) (assuming the parameter has been named 'object_model' in the function definition).

Both functions can change the current loop interval setting by returning a value that can be interpreted as numeric and greater than zero. It can be fractional, but values less than about a second are not recommended.

The whole daemon.py file is (re-)imported each time the routine notices it having changed, so whatever is outside any functions will run once at import (before setup() is run) so can include imports and global variable definitions.

Thus, for example, daemon.py could be:

# example daemon.py file
#

# setup() is called once, with dict-of-dicts of object model as sole parameter
# if this function returns a value that can be interpreted as a number > zero
# the loop interval will be set to that value (seconds)

def setup(om):
    global tlog
    tlog=open('/opt/dsf/sd/sys/tempslog.csv','w')
    print (om['boards'][0]['uniqueId'], file=tlog)
    return(30)

# loop() is called periodically, with dict-of-dicts of object model as sole parameter
#
# at each next occurrence of a multiple of the interval since the epoch,
# the object model dict is updated and then this function is run
#
# if this function returns a value that can be interpreted as a number > zero
# the loop interval will be changed to that value

def loop(om):
    global tlog
    print(om['state']['time'], end='', file=tlog)
    for h in om['heat']['heaters']:
        print (','+str(h['current']), end='', file=tlog)
    print(file=tlog, flush=True)


    if om['heat']['heaters'][1]['active'] > 0:
        return(3)
    else:
        return(30)

This will create a 'tempslog.csv' file in the printer sys folder, and log the time and the temperature of each heater into it in CSV format. If heater 1 is set to a target value greater than zero, the log will update every three seconds, otherwise it will update every 30 seconds. If you make any change to daemon.py (including e.g. simply touch daemon.py at a command prompt on the Pi) the plugin will notice a change to the file, and re-run setup(), creating a new tempslog.csv and obliterating the previous one. You can also simply rename daemon.py to something else to stop it running, and name it back to daemon.py when you want the logging to run, or stop and start the plugin.

(If you didn't want 'obliterating the previous one', it would be a case of changing the file open command in setup() to tlog=open('/opt/dsf/sd/sys/tempslog.csv','a') so you append to the .csv file rather than write to it.)

Multiple loop functions can be defined, with names in the format loop<nn> where <nn> is an arbtrary integer, e.g. def loop13(om):. These will run every nth loop (e.g. every 13th loop). At each interval the bare loop() function runs first, and then each relevant loopn() function is run in the order that they are found in the daemon.py file. For example, to add a line of headers repeated every 20 lines of data, you could add to the example above:

def loop20(om):
    global tlog
    print ('"time               h0    h1    h2"', file=tlog)

Although loop() runs before any loopn() function, you can circumvent that by defining loop() as just pass and then defining e.g. a loop20() earlier in the daemon.py file than a loop1(). On most increments loop() will go first and do nothing then loop1() will run, but on every twentieth increment loop() will run and do nothing then loop20() and finally loop1() will run.

As a further variant on this, you can name a loopn() function beyond the number, so two different functions that both run every 20 intervals could be named loop20a() and loop20b() (or loop20tweedledum() and loop20tweedldee(), or whatever).

All these additional loopn() functions also need to take a single parameter (which will be the object model) and can change the interval timer by returning a numeric value.

As implied above, the daemon.py file can be removed and replaced or changed at will and the plugin should handle it gracefully. It will fail and the plugin will stop running however if while editing the file it's saved in an intermediate non-python-grammatical state at the moment the plugin tries to run it.

To see messages relating to the plugin run journalctl -u duetpluginservice -f at a command prompt on the Pi.

The logged messages can be greatly increased by setting 'verbose' and 'vTS' to True in the top of file /opt/dsf/plugins/PyDaemon/dsf/pydaemon.py on the Pi. 'vTS' adds a microsecond-resolution timestamp to each logged comment.

It's not very extensively tested.

To install:

You need dsf-python installed. At a command prompt on the Pi: sudo pip3 install --break-system-packages --pre dsf-python. It will moan about how you should be using a virtual environment instead, but should work. I haven't done any testing with virtual environments. Note the '--pre' is because dsf-python is currently pre-release for 3.5 firmware.

Otherwise I don't think it needs any very non-standard modules - it uses json, time, sys, pathlib, importlib, re and inspect, which are probably all in by default (but I can't swear to that). If something complains you might need to install the relevant module.

You should read the source to ensure it's not doing anything nefarious. It's about 200 lines of pure python (and about 100 lines of comments).

To install the plugin drop the zip onto the 'Install Plugin' button in Plugins / external plugins in DWC and click the Start button. Then (or previously) create your daemon.py file in the printer sys folder (on the Pi: /opt/dsf/sd/sys)

As usual, I warrant nothing. It's not even fit for any purpose.

You'll need to remove the .txt, this is just me circumventing the forum systems: download: PyDaemon.zip.txt

This is my prototype.

I've had problems with enclosure overheating before (at least, that's what I blamed my problems on), so I'm maybe oversensitive to it, but my thinking was an extract fan at the top of the enclosure could draw out hot air, but that a fan alone at the top of the enclosure would act as a chimney even when I wanted the air to stay put, so I wanted some means to block that convection.

However, I emphasise it's all just hypothetical speculation at the moment - the printer and enclosure isn't built yet.

Here it's just on a servo tester, but (as noted up the thread) I have had it running on the Duet.

This is printed in PLA - it would want something more robust for a high temperature enclosure, or your shutter blades would droop into the enclosure. You might be able to laser cut them from aluminium though and put a bolt through the gears as the pivot, if you want a decent temperature - they are three flat parts slotted together.

@piotrkmiotczyk there are layers and layers of 'why'.

Why you connect a homing switch on a 3D printer so that it's normally 'on' (ie the input is normally tied to ground) is as chrishamm says - so that if it becomes disconnected the machine stops because it thinks it's at the endstop.

Why the 'normally on' is to ground (rather than to +ve supply) is because that's how the Duet boards are designed - there's a pullup resistor on the input so a disconnected switch goes to +ve (actually 3.3V), so you need to arrange the switch connected to ground (0V). See e.g. this snippet from the Mini5 schematic:

Here IO_0 to the left is what goes to the chip, and IO_0_IN to the right is what goes to the pin on the connector. The R117 is the pullup resistor, so if the switch is open the chip 'sees' 3.3V, and if the switch is closed (and connected to 0V) the chip 'sees' 0V. If you connected the switch to 3.3V, the chip would always 'see' 3.3V.

Why the boards are designed that way is (probbaly) because that's the normal way it's done - most microprocessor switch inputs are configured this way, with a switch and resistor arranged that when open the chip sees +ve supply due to a pullup resistor and the switch connected to ground so that when the switch is closed the chip sees 0V. See most Arduino or Raspberry Pi or similar introduction to electronics tutorials - this is how it's normally done.

Why this is normal is - dunno. Possibly it's because you more normally have multiple 0V points and lines on a board so it's often easier to get a 0V wire / signal to a switch than it is to get a +ve supply wire. There's often no really good reason - if you were designing the circuit yourself you could use a switch with a pull-down resistor and the switch connected to +ve - then the chip would see 0V when the switch is open, and +ve supply when the switch is closed.

Some chips have built-in pullup resistors, so with this configuration you don't need a separate external resistor, but I think that's mainly because this is the normal way it's done. That is, the chip designers have done that in reaction to this being the normal approach, not that this is the normal approach because that's how the chips are designed. (Some chips have both pull up and pull down - and some have differnet strengths in each direction, but again, I think that's a result not a cause.)

Also, many (and I think probably most) configuration inputs to chips are arranged like this so 0V means 'active' - for example chips that have a 'select' line to make them do something are often/usually designed so that making that input 0V selects them. It will normally be shown as 'CS' with a line across the top of letters - meaning 'chip select active low' (because the letters are below the line, ie low). Or reset lines are often designed to reset the chip when the input is forced to 0V. The chips on the Duets show that too, see e.g.:

So here, the chip resets if that input is forced to 0V, so the board has a resistor (R47) pulling it up to 3.3V and there's a switch that forces the line to 0V when it is closed.

This does have some good reasons behind it (to do with asymmetries in semiconductor physics - much the same ones as to why we normally use low side switching transistors), but only for early chip designs (mostly obsolete). However, early chips did it that way for good reasons, and newer chips do it that way because that's the way the all the other chips do it.

@vistalert said in Height Map - 500mmx500mmx4mm aluminium build plate:

any chance you can run that with 4mm for me?

No need.

It will be a linear elastic analysis (you're not working the plate hard enough to worry about any plasticity) so the deflection will be proportional to applied load per unit area, and inversely proportional to the section modulus per unit width. Section modulus per unit width is proprtional to thickness cubed.

So an analysis for 5mm plate can be turned into an analysis for 4mm plate by multiplying by 4/5 to account for the self weight changing, and dividing by (4/5)^3 to account for the section modulus changing. (Note that the 5mm to 4mm change basically halves the stiffness of the plate - (4/5)^3 = 0.512)

Thus, a 0.06969mm deflection due to self weight for a 5mm plate would become a 0.10889mm deflection for a 4mm plate.

The additional 0.01016mm deflection due to additional 500g would just get the stiffness ratio modification (assuming you're still planning on adding 500g) so becomes 0.01984mm, giving a total of 0.08953 (c.f. 0.07985).

As a (really very rough) approximation, deflection remaining under half thickness ought to keep you in the elastic regime, so this is still valid.

HOWEVER, I have some pretty big quibbles with that analysis. I think what has been analysed is not appropriate to your case.

The contour key is illegible, but assuming that it runs to zero at the dark blue, it's clear that there are very large flat areas at the corners. This is not a plate resting on supports at the corners - it's clamped by something very stiff (in the analysis, probably infinitely stiff) across a relatively large part at each corner. So instead of a single sagging curve, you've got a reversing curve profile - the plate is hogging at the corners, then sagging through the middle of the span. This will result in much less deflection than a case where it's actually just resting at the corners (or clamped with something not very flexurally stiff - like a single smallish bolt).

If you look at your probed heightmap, you've got a shape with sharp pinnacles at each corner. This analysis doesn't have that - it has round-topped rolling crest, with a large, flat, (uniform blue) expanse.

I've done a an analysis of a 500x500 4mm thick plate from 5083 alu (actually, just from iostropic uniform material E=72GPa, poisson=0.33, which is pretty close to 5083 alu).
Alu is 2700 kg/m3, which is 27 kN/m3. Therefore 4mm thickness is 0.108 kN/m2 or 0.108kPa.

I get 0.401mm centre defelection, which is not far off your height map result.

If I generate a contour plot, with contours on the deformed shape, deflections being multiplied 700 times, I get something visually really not at all dissimilar from your height map:

A 6mm plate will be 3.4 times stiffer than the 4mm plate, will have 50% more load, but the combined effect will be under half the self weight deflection (all other things being equal), and the deflection under a given imposed load will be under a third (1/3.4).

I'd go for at least 6mm plate. Actually, my 300mm diameter delta bed (supported at 3 points) is 6mm plate.

There are devices intended for bolt mounting, e.g. https://www.digikey.com/catalog/en/partgroup/b12-series/6415

It occurred to me to check some other input shapinng:

M593 P"zvd" F37 clunks more softly and at different movements: in the 1200 acceleration case (which clunks under zvddd other than 12-26) it clunks for movements above xval=22

M593 P"zvdd" F37 clunks intermediately loudly, but at different movements: in the 1200 acceleration case (which clunks under zvddd other than 12-26) it clunks other than xval=8-24

So I also tried varying teh frequency

M593 P"zvddd" F74 and M593 P"zvddd" F18 both clunk and not-clunks differently to F37

@droftarts Aha! Excellent, thank you. I was just about to figure out how to try it standalone, following @Phaedrux 's request. I confirm that if I run mine SBC mode without input shaping I have no clunks. Since the cause has been narrowed this far and repeated by someone else, I'm not inclined to work back through old firmware versions, unless really likely to make teh difference between solving it and never resolving it, but I could try some older versions if it will make a big difference to tracking down the problem - please let me know.

Input shaping as the 'cause' stacks up because I only relatively recently put on a toolboard, and it's only when I got the toolboard (with the accelerometer) that I enabled input shaping. So although I hadn't made the connection that that's when clunks started, with hindsight it's very credible it was at about that time. I don't run it fast enough to really need input shaping anyway - the quality enhancement is debatable, and it's more a case of enabling it because it's there, so disabling it is not a hardship.

Thanks everyone for input, I'm now clunk free (though I also have a printer in pieces, so I need to spend some time re-assembling).

@droftarts no, no config-override.

I've tried taking teh test case that clunks and rotating it 120 degrees about the global z-axis, and running taht to see if teh X tower motor then clunks. All teh moves are then teh same relative to X tower as teh clunking case were relative to Z tower. However, when I do that, nothing clunks.

This is my rotated test case:

; test clunking for varying coordinates
; rotated 120 degrees about Z

G1 X56.292 Y32.500 F9000
G4 P100
G1 X43.292 Y55.017

G4 S3

G1 X56.292 Y32.500 F9000
G4 P100
G1 X42.792 Y55.883

G4 S3

G1 X56.292 Y32.500 F9000
G4 P100
G1 X43.292 Y55.017

G4 S3

G1 X56.292 Y32.500 F9000
G4 P100
G1 X42.792 Y55.883

G4 S3

@Phaedrux it's on the Z-tower motor, regardless of which physical motor or which driver that is. I've tried three different motors and four of the drivers on the 6HC board, in various combinations, whatever is defined as Z-tower motor clunks. The motors and drivers that clunk when they are Z do not clunk when they are X or Y.

@droftarts I've tried playing with accelerations, and there's a clear correlation, but not a helpful one (not one that lets me avoid the clunk).

To recap: with accelerations = 1200, at Y=-65, it doesn't clunk for movements to X=12 to X=26 inclusive, but does for all other coordinates.

I've tried various other accelerations and there is clearly a correlation. This is maximum (orange) clunk-free movement and minimum (blue) clunk-free movement against acceleration. So no clunk between the lines, but clunks outside them.

(at A = 300 I can't detect any movement at all at the lower limit, clunking or not)

I note that you refer to bearings sticking - I have none, the motor clunks with nothing connected, so I'm confident it's not mechanics-related (i.e. not bearings, belts, interference, etc).

I've taken a video to show the difference between clunk and noclunk - there's no mistaking whether it clunks or not, the video is playing a move to 26, then one to 27, then one to 26, then one to 27. This is with the original 1200 acceleration where 27 clunks and 26 does not: https://vimeo.com/955477735

; test clunking for varying coordinates

G1 X0.00 Y-65 F9000 
G4 P100
G1 X26 Y-65

G4 S3

G1 X0.00 Y-65 F9000 
G4 P100
G1 X27 Y-65

G4 S3

G1 X0.00 Y-65 F9000 
G4 P100
G1 X26 Y-65

G4 S3

G1 X0.00 Y-65 F9000 
G4 P100
G1 X27 Y-65

G4 S3

@droftarts thanks. I'm out of reach of the machine for a couple of days, so it will be a little while. I don't think you'd miss the clunk if it occurred - it's enough to make the print head visibly quiver on my printer.

I'm using code such as:

G1 X0.00 Y{var.yval} F9000
G4 P100
G1 X{var.xval} Y{var.yval}

wrapped in a loop altering xval or yval.
The clunk happens at the end of G4 or start of the second move (which I find slightly odd, because it means where the move ends affects the behaviour at the start of the move).

This is what I've tested so far (xval across the page 5 to 99 and yval down the page -40 to -99). So far, if a given yval value clunks, it clunks at the same xval values, being 5 to 11 and 27 to 99 inclusive. Red is a clunk, blue is no clunk, white is untested.

@droftarts Hello. 3.5.2-rc.1 also clunks, and in all the tests I've redone it clunks or not-clunks for teh same coordinates as 3.5.1.

@achrn said in delta Z motor goes clunk, regardless of motor or driver:

It clunks at whatever X coordinate is in the second move, as long as it is enough that the motor moves.

Ha! That's not true.

G1 X-5.00 Y-64.00 clunks
G1 X-6.00 Y-64.00 clunks
X-7 to -11 all clunk

G1 X-12.00 Y-64.00 does not clunk
X-13 to -26 all do not clunk

G1 X-27.00 Y-64.00 clunks
-28 to -69 all clunk

The pattern is same for positive X numbers, i.e. G1 X5.00 Y-64.00 clunks, G1 X12.00 Y-64.00 does not clunk, G1 X27.00 Y-64.00 clunks etc. all the way up to X99

@o_lampe thanks for thoughts. Yes, 64,64 (with any combination of signs) is well within the bed. Bed is 150 radius, with 0,0 at the centre and standard 120 degree spaced towers.

It clunks at whatever X coordinate is in the second move, as long as it is enough that the motor moves. That is, because this is the Z motor at X=0 it isn't actually turning. If the second move is G1 X-1.00 Y-64.00 there is no clunk, but the motor doesn't move at all (it's a theoretical move of less than a quarter of a microstep). If it's G1 X-5.00 Y-64.00 (which is 5.8 microsteps of the motor - I don't know whether that will actually apply 5 or 6) it clunks (though more weakly).

I've also found it clunks for Y= +/- 32 but not for Y= +/- 16 or Y= +/- 128. I'm going to do some more investigation about what coordinates trigger a clunk.

It clunks for any value of Z, whether Z is specified or not, and indeed for any motor position - if I home it to a random position (i.e. so the physical position of the motors is not what they would be when properly homed) it still clunks at the same coordinates.