A Software Solution to Eliminate Ringing?

[A Former User]

@DigitalVision
Wow - would be great to have this optional sometime in the future! Would be great to have beside the option to calculate the val the "old" try-n-error option to print a tower with diffrent "zeta"-val...

Have you been aware of this project I just read about today (?): https://www.ulendo.io (which seems to do for the avarage-joe what create-it-real does for OEMs since years)

Just exploring all this for me new stuff, I stumbled across "Helling-Bestehorn" (the "smooth-runner") and "Polynom of the 5th order" which seems to be an "allrounder" in terms of motion-control - would really like to hear your opinion on it...

Congrats & Cheers & all of it

[DigitalVision]

@LB said in A Software Solution to Eliminate Ringing?:

@DigitalVision
Wow - would be great to have this optional sometime in the future! Would be great to have beside the option to calculate the val the "old" try-n-error option to print a tower with diffrent "zeta"-val...

Thanks. Calibrating the f_n is actually really easy using a similar approach to my proposed method of calibrating pressure advance. You print a simple test print varying the f_n parameter layer-by-layer. You will see a very clear phase inversion in the ringing pattern at the point that corresponds to the right f_n number and you can simply measure the height of that inversion to find the right value. That's how I determined the f_n = 40.4 Hz value above. A less accurate / coarse method is to measure the ringing spacing (peak-to-peak) at known print speed. In this case, 80 mm/s print speed, 40 Hz natural frequency corresponds to 2mm peak-to-peak spacing.

Just exploring all this for me new stuff, I stumbled across "Helling-Bestehorn" (the "smooth-runner") and "Polynom of the 5th order" which seems to be an "allrounder" in terms of motion-control - would really like to hear your opinion on it...

I've not heard about Helling-Bestehorn – seems like a sinusoidal interpolation basis function. For smooth interpolants that satisfy a continuous curvature constraint (e.g. continuous centrifugal force) a 5th order polynomial is the most straightforward choice. You have 6 coefficients that you solve by 6 constraints: at each end you fix the position, velocity and curvature and you get a simple closed form solution for the polynomial coefficients. I've looked at this to smooth tessellated paths into a continuous curve.

[A Former User]

@DigitalVision said in A Software Solution to Eliminate Ringing?:

@LB said in A Software Solution to Eliminate Ringing?:

@DigitalVision
Wow - would be great to have this optional sometime in the future! Would be great to have beside the option to calculate the val the "old" try-n-error option to print a tower with diffrent "zeta"-val...

Thanks. Calibrating the f_n is actually really easy using a similar approach to my proposed method of calibrating pressure advance. You print a simple test print varying the f_n parameter layer-by-layer. You will see a very clear phase inversion in the ringing pattern at the point that corresponds to the right f_n number and you can simply measure the height of that inversion to find the right value. That's how I determined the f_n = 40.4 Hz value above. A less accurate / coarse method is to measure the ringing spacing (peak-to-peak) at known print speed. In this case, 80 mm/s print speed, 40 Hz natural frequency corresponds to 2mm peak-to-peak spacing.

Ah! I have really problems with a big printer I build a while ago with ca. 1x1meter with "springiness" of the belts and axis because of ca. 5kg mass (but it has less then 0.01mm bending by gravity in the middle...) in x & y, so that the max. jerk setting ist pretty low for now, and this could help I guess to be able to make it faster all round without wobbling/ringing one day! Would be great if the z-axis is taken out of the equation in a first aproache and just have x&y separate, since on most cartesian printers those are unequal from the buildup.
So if you can tell me how to support you I try my best, e.g. I can offer bavarian beer or you open a patreon-page or similar?

Just exploring all this for me new stuff, I stumbled across "Helling-Bestehorn" (the "smooth-runner") and "Polynom of the 5th order" which seems to be an "allrounder" in terms of motion-control - would really like to hear your opinion on it...

I've not heard about Helling-Bestehorn – seems like a sinusoidal interpolation basis function. For smooth interpolants that satisfy a continuous curvature constraint (e.g. continuous centrifugal force) a 5th order polynomial is the most straightforward choice. You have 6 coefficients that you solve by 6 constraints: at each end you fix the position, velocity and curvature and you get a simple closed form solution for the polynomial coefficients. I've looked at this to smooth tessellated paths into a continuous curve.

Ah - have to dig deeper one day I guess - currently over the top for me - thanks anyway for now!

[DigitalVision]

If this method will turn out to be useful, here’s what I think the likely end-state (at least as far as I can see) is for 3D printer motion control.

To replace instantaneous velocity change to handle segmented curves in a continuous motion, it is likely that we need a way of defining smooth (G2 continuous) profiles. Using some type of spline representation is probably the best choice, and out of the different representations NURBS is the most obvious one, since it has a number of good properties like the ability represent conics (like circular arcs) exactly. We can certainly get away with something slightly simpler than NURBS, but the difference in complexity is hardly significant.

Afaik, there is no good spline representation that has a straightforward arc-length parametrization though, something we need to effectively generate physical motion profiles (and achieve C2 continuity). The best path is probably to create a re-parametrization through a second approximating spline (approximating the inverse of the arc-length function).

With this we can generalize the current motion primitives (line segments, arcs), support transition curves and other smoothing primitives including the ability to represent (and possibly reconstruct) the original curved surfaces that were used to generate tessellated polygonal/STL representations.

With S-curve motion, acceleration planning would be the job of defining (at a minimum) a piecewise linear acceleration profile over the arc-length parameter ensuring adherence to all motion limits. Higher orders than 3 may be valuable to model more complex compounded spring-damper systems, but lacking any proof of that a 3rd order model seems right.

So we get effectively 4 functions:

1. From the motion planner, we get a (at minimum piecewise-linear and continuous) function a(t), that when doubly integrated gives a mapping s(t) from time t to arc length s.
2. From the inverse arc-length-approximating spline, we get another mapping q(s) from s to the NURBS parameter q.
3. From the NURBS profile we get the mapping from q to the spatial dimensions {x,y,z,e,…}
4. From the spatial dimensions we apply model-based control (spring-damper correction) and machine configuration to get final actuator axes positions.

A somewhat complicating factor is that I believe today there is a tight coupling from 4 back to 1. Motion constraints defined in actuator space feed back to the motion planner. With today’s simple motion primitives these constraints can probably be expressed in closed form with respect to the acceleration profile, but I don’t think that’s going to be easy or even possible with the above scheme. One option (a) is to decouple this by providing (or calculating) sufficient guard-rails to the spatial constraints for the motion planner that machine constraints don’t need to be considered. Another option (b) is an iterative process feeding back e.g. Taylor-approximations of the constraint mappings.

The nice thing about option a is that it simplifies the implementation significantly, and with some limitations even allows 1-3 to be computed offline. That’s effectively what I did above but with a much simpler geometric profile. I also included the model parameters for the spring compensation though, which unfortunately makes the output incompatible with the model-based control RRF already does for extruder pressure advance, so I had to disable that.

For prototyping I can fairly easily hack 1-3 together, creating a time-parametrized motion profile. I wonder how to best feed that to RRF is though. Since RRF supports constant acceleration segments already, they’d be great candidates to approximate the profile. I.e. pairs of M204 (acceleration limit) and G1 commands to describe the path. For this to work with high segment rates, I’d probably need to hack the firmware a little bit to bypass the motion planner and instead have it follow the provided motion profile exactly, although I’d love to hear if there are better options.

[dc42]

What I have in mind is that when the GCode involves a change in direction between adjacent printing moves, RRF will insert a joining move between them. This joining move would be a quadratic or cubic in shape, and would deviate from the path specified in the GCode by no more than a user-set deviation parameter. So an internal corner would be cut by no more than this amount. Different motors would be executing trajectories of different shapes during this joining move.

[bot]

@dc42 @DigitalVision

Why don't we use an approach that has already been implemented and proven in Klipper firmware? It sounds similar.

Described here: https://onehossshay.wordpress.com/2011/09/24/improving_grbl_cornering_algorithm/

First let’s assume that at a junction of two line segments, we only look at centripetal acceleration to simply things. In other words, we assume the tangential velocity is zero and the velocity through it is constant. At the junction, let’s place a circle with a radius R such that both lines are tangent to the circle. The circular segment joining the lines represents the path for constant centripetal acceleration: junction = sqrt (a max R) [See URL for correct forumlas]. Where the maximum junction velocity v junction is the fastest speed the CNC can go through the junction without exceeding the CNC’s maximum allowable acceleration a max.

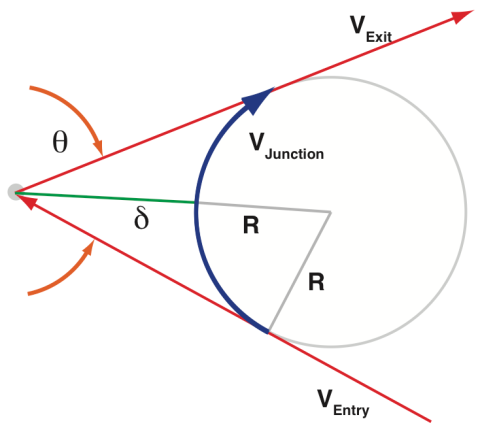
This circular segment creates a virtual deviation from the path delta, which is defined as the distance from the junction to the edge of the circular segment. This delta parameter is defined by the user as a setting, which indirectly sets the radius of the circle, and hence limits the junction velocity by the centripetal acceleration. Think of the this as widening a race track. If a race car is driving on a track only as wide as a car, it’ll have to slow down almost to a complete stop to turn corners. If we widen the track a bit, the car can start to use the track to go into the turn. The wider it is, the faster through the corner it can go.

A note on the Klipper implementation:

However, in Klipper, junction speeds are configured by specifying the desired speed that a 90° corner should have (the “square corner velocity”), and the junction speeds for other angles are derived from that.

More info on the Klipper firmware: https://www.klipper3d.org/Kinematics.html

[DigitalVision]

@bot said in A Software Solution to Eliminate Ringing?:

@dc42 @DigitalVision

Why don't we use an approach that has already been implemented and proven in Klipper firmware? It sounds similar.

This approach is certainly the easiest one, especially in a firmware that already supports arcs, but the problem is that this method doesn't preserve a continuous curvature. There is an abrupt change in curvature going from the smooth line to the circle, something that would yield an instantaneous position change with spring-damper compensation.

In road and railroad construction you never build curves like that for the same reason. You would have to turn your steering wheel instantaneously to a new position to follow such a path. What civil engineers do instead is add a transition curve (a spiral shape) that creates a gradual increase in curvature.

With a polynomial spline (like @dc42 suggests) we can create a curve that has a gradual curvature.

[bot]

@DigitalVision interesting. Thanks for the explanation.

That makes sense. Instead of the G1 curvature, it might be G2 or G3?

I'm not as smart as you two when it comes to these algorithms, so I'll keep to myself now. I just get worried when there is talk of the firmware injecting intentional deviation into the stream. I'll have to wait and see results, I guess!

[Edit: Just to clarify, the Klipper method does not actually deviate from the path -- it is only a virtual deviation to calculate the speed change possible.]

[DigitalVision]

@dc42 said in A Software Solution to Eliminate Ringing?:

What I have in mind is that when the GCode involves a change in direction between adjacent printing moves, RRF will insert a joining move between them. This joining move would be a quadratic or cubic in shape, and would deviate from the path specified in the GCode by no more than a user-set deviation parameter. So an internal corner would be cut by no more than this amount. Different motors would be executing trajectories of different shapes during this joining move.

In order to satisfy a smooth curvature (G2 continuity) at both the start end end of such a joining segment, I you either need a higher order polynomial than quadratic or cubic or you need to piecewise combine multiple polynomials. An easy way to think about it is that a cubic polynomial only has one point where the second derivative is zero and you need two. For a single polynomial to describe a symmetric transition curve, I think you need a 4th degree (quartic) polynomial, and for a generic transition between two arbitrary points the degree increases to 5 (quintic?).

Another important property that we want for a smoothing method is to allow for constant arc-length speed. I.e. the print head should be able to move through a circle made up of line segments at constant extrusion speed. This means that ideally you want the curve to be parametrized based on arc length. For a circular arc this is trivial, but it's not so easy for a polynomial curve shape. That's the reason I suggested a second inverse-arc-length approximating polynomial.

In the extension though, if you implement say a spline of 3rd order polynomials to support joining moves you've basically done 90 % of the job of supporting a general spline motion profile. And going all the way has some very nice properties. The slicer could now output perfect arc and elliptical shapes, and replicate more generic curve shapes out of most CAD software perfectly. I believe this is where the industry is going for advanced CNC control paths.

[DigitalVision]

@bot said in A Software Solution to Eliminate Ringing?:

@DigitalVision interesting. Thanks for the explanation.

That makes sense. Instead of the G1 curvature, it might be G2 or G3?

That's right. In the end, we actually need C2 continuity, but if you start with G2 you can reparametrize it to achieve C2.

I'm not as smart as you two when it comes to these algorithms, so I'll keep to myself now. I just get worried when there is talk of the firmware injecting intentional deviation into the stream. I'll have to wait and see results, I guess!

You bring up some good questions. The intentional deviation may sound controversial, but it's actually the reality already. I don't know of any high-end professional CNC machine that doesn't do this (since it significantly increases the motion speed), and that's generally an application with much tighter tolerance requirements. In the case of joining line segments and doing spring-damper compensation the outcome is actually a more faithful reconstruction of the original curve.

You could make a valid argument that the smoothing should be done by the slicer instead of the firmware. I don't have a strong opinion either way. I think the reality is that a lot of the way our current pipelines are constructed just kind of happened and making a local change is much easier than driving a change across softwares. For example there is no good reason a slicer should need to know what your filament diameter is.

If smoothing were implemented in firmware, I would expect it to be controlled by a cordial error tolerance parameter that you could set to zero to disable the behavior.

[Edit: Just to clarify, the Klipper method does not actually deviate from the path -- it is only a virtual deviation to calculate the speed change possible.]

Thanks, that makes sense.

[bot]

I've been modifying PrusaSlicer for the past few months as a way to slowly learn and get used to how it works under the hood. My end goal is to make sure the slicer and firmware are playing nicely together. If you want to try and put some of this smart stuff into PrusaSlicer, maybe just for testing, I'd be glad to lend a hand with the tedious bits or pointing you around the codebase as best as I can.

I do get worried at the thought of the firmware having more calculation overhead. Once we solve the "jerk" problem, and we can round corners faster, then we solve the ringing problem, we'll quickly encounter the next problem: too many segments too fast.

[CCS86]

Great thread!

I am very interested to see this progress.

[theruttmeister]

@DigitalVision said

You could make a valid argument that the smoothing should be done by the slicer instead of the firmware. I don't have a strong opinion either way. I think the reality is that a lot of the way our current pipelines are constructed just kind of happened and making a local change is much easier than driving a change across softwares.

The only argument I can see for accepting implementation in the slicer is if the processing overhead is so huge that it cannot be done in firmware.

Adding it to the firmware keeps the firmware slicer agnostic.
It also means people using RRF for non-FFF projects can use the functionality.
And just like bed-leveling, its a per-machine setting. If you are running a printfarm, its a nightmare to have to deal with machine specific slicing profiles.

For example there is no good reason a slicer should need to know what your filament diameter is.

Very true. I think that's mostly due to legacy slicing function. I know there's no firmware reason to keep working like that.

[DigitalVision]

A short update.

I managed to get some hours to spend on this today, so I rewrote the test code from before mostly from scratch and turned it into a G-code filter. I can now take a regular slicer output file, pass it through the filter and feed the result to the printer. This makes it easier to do realistic testing. The code only really supports linear paths to far, so curves with high tessellation counts will end up looking terrible, but it should work OK for calibration cubes and similar objects. In the process of rewriting it I also implemented some improved machine limits so I won’t have to worry about it trying to move the Z-axis on my cartesian printer at 120 mm/sec.

Here are some quick-and-dirty results.

speed: 80 mm/s, accel: 10 m/s² (10,000 mm/s²), jerk: 2 km/s³ (2,000,000 mm/s³)

I'm actually pretty happy with that given that this is a 490 g heavy end effector on 375 mm diagonals. For reference, here's what it looks like without any spring-damper compensation:

speed: 80 mm/s, accel: 5 m/s² (5,000 mm/s²)

Pushing it a bit faster.

speed: 120 mm/s, accel: 20 m/s² (20,000 mm/s²), jerk: 2 km/s³ (2,000,000 mm/s³)
Some extrusion glitches, but not much ringing.

I’ll share the code once I’ve written a little documentation on how to use it as I’d love to get some more testing and learnings.

[CCS86]

@DigitalVision said in A Software Solution to Eliminate Ringing?:

A short update.

I managed to get some hours to spend on this today, so I rewrote the test code from before mostly from scratch and turned it into a G-code filter. I can now take a regular slicer output file, pass it through the filter and feed the result to the printer. This makes it easier to do realistic testing. The code only really supports linear paths to far, so curves with high tessellation counts will end up looking terrible, but it should work OK for calibration cubes and similar objects. In the process of rewriting it I also implemented some improved machine limits so I won’t have to worry about it trying to move the Z-axis on my cartesian printer at 120 mm/sec.

Here are some quick-and-dirty results.

speed: 80 mm/s, accel: 10 m/s² (10,000 mm/s²), jerk: 2 km/s³ (2,000,000 mm/s³)

That is a beautiful print!

[PCR]

@theruttmeister

Only a quick thought. I really like the idea of a slicer setting for that.
I am using KISSlicer alot with the PreloadVE feature. In the end the machine do not know how the 3D model look. So i think the best approached is a hybrid one!

[theruttmeister]

@PCR
Its always going to be hybrid.

I would make the case that this specific thing (software compensation for position error) is about getting the printer to actually do what you told it to do. If the printer was more rigid, the function would not be needed. Therefore, it falls into the same category as basic things like steps per mm.
And it has applicability for any motion control done with RRF/Duet, not just FFF.

Functions like Preload in KISSlicer (not that I have used it), are material specific, not just machine specific. So it has to be in the slicer to work correctly.
And its a function that only works for FFF.

@PCR said in A Software Solution to Eliminate Ringing?:

@theruttmeister

Only a quick thought. I really like the idea of a slicer setting for that.

For what?

If you mean filament diameter, my point was that we could be using a volumetric value, people don't because there's no real advantage to it and we all got into the habit of futzing with the slicer setting to get certain effects... But if most printers had an accurate device for measuring filament diameter as it went into the extruder, it would produce more accurate prints.
Not to a degree that I think most people would notice though. Which is why its not a thing.

[DigitalVision]

Another update.

Before sharing the python code, I wanted to test it on at least one other printer. This time on a cartesian (CoreXY) printer with CPC linear rails. The printer x-axis is made up of one single 15mm rail with a sole runner block holding the hotend and extruder assembly. The rail itself is very rigid. The weak point is instead the x-axis carrier/runner block that has a bit of yield to its roll axis (resulting in ringing along the y axis).

In getting the calibration done for this printer I learned a number of new things. First, and very importantly there are actually two modes of ringing. The first one is the one we classicality think of as ringing. It occurs after the printer has decelerates down to a full stop and the end effector oscillates. The photo below illustrates this.

The second type of ringing was something I hadn’t considered before. It’s ringing that happens during the acceleration phase. If you look carefully you can see it happening in the simulation in the first figure in https://www.digitalvision.blog/spring-damper-control. The effect may look subtle in that animation, but the result on an actual print is much more substantial. The effect is that the extrusion bead gets stretched and compressed periodically.

The effect of this is what I suspect often prevents getting consistent extrusion when printing at high speeds. The extrusion gets ripped apart in the stretching phase. After correcting for this ringing I’ve been able to print consistently even at 150 mm/s with 10 m/s² accelerations, something that I’ve never managed before.

When observing ringing on a print, you will often see a compound effect of both of these two modes of ringing, with the acceleration ringing from e.g. the x-axis compounding with the post-deceleration ringing from the y-axis. When the two axes have different natural spring frequencies the two axis parameters can be hard to tease apart. For that reason, I came up with the strategy of isolating one axis at a time by setting the acceleration limits of the other axis to a very low value. E.g. 10 m/s² acceleration on the y axis with 0.5 m/s² acceleration on the x.

My final issue with calibrating this printer was that I was unable to find a single setting that eliminated the ringing on both the left and right side of the print. The left side had a ringing frequency of ~52 Hz with the right side closer to 60 Hz. It seems like the ringing had different frequencies when moving in the positive y direction vs the negative. Thinking a bit about this I came up with a model that makes sense. The print head is not perfectly balanced under the axis with the center of gravity being offset to one side. This effectively means that gravity is applying pre-tension on the spring biasing the spring effect towards one direction. To test this hypothesis I implemented an asymmetric spring model and plugging in 52 and 60 Hz respectively for the two axes did the trick.

[DigitalVision]

Here's the python test code if anyone wants to give this a shot.

https://github.com/OskarLinde/dynamic-motion

The link contains some preliminary instructions for how to use and calibrate the method. You need at least RRF 2.03 since without the M566 P1 jerk policy the G-Code doesn't execute reliably. I was able to run this on an unmodified firmware for simple objects, but found that I could increase the discretization points and run more complex objects if I made a minor firmware change: I disabled the motion planner (look_ahead) if the current move speeds were below the current instantaneous velocity change settings. With this, the extrusion issues in the 120 mm/s print went away. Oh, I also implemented pressure advance correction the script since the firmware one doesn't work with the type of G-Code the script outputs.

While there are many limitations as described above I'd love to get some testing of this approach: Were you able to get it to work? Were you able to see any improvements in ringing or improvements in print speeds? What type of printer and what calibration values did you land on?

[sebkritikel]

Despite the fact my machine is half disassembled, and the fact I recently swapped out extruder motors without much 'calibration' this has been pretty cool to work with. I don't think I have anything workable yet, but still neat to play with. Once I get my machine put back together, hopefully I'll be able able to work through the parameters more methodically.

A quick note - I'm thinking the z_max (in mm) parameter is a bit wonky, initially I did some thin wall prints that were 100mm tall, and could only see variation (both in Craftware for previewing) and in the print for the first 20mm or so - even if I set z_max to 100. When I set it to 20mm (for a 20mm tall print) it also looks like the variation occurs in the first 5-8mm or so.

Ok, testing was done on an IDEX machine (only with T0). Fairly heavy Y gantry that carries the T0 and T1 print heads, plus X and U steppers. A quite large print bed, so I modified the python files to eliminate changes to the Z axis (had some issues during my first few tests). I get some significant defects due to the bed oscillating on layer changes. Some potentially useful information from the config.g

M92 X100.00 Y96.00 Z1280.00 U100.00 E415.00        ; Set steps per mm

M566 X1000.00 Y1000.00 Z500.00 U1000.00 E36000.00         ; Set maximum instantaneous speed changes (mm/min)
M566 P1

M203 X18000.00 Y18000.00 Z1320.00 U18000.00 E3000.00     ; Set maximum speeds (mm/min

M201 X4000.00 Y4000.00 Z450.00 U4000.00 E3000.00         ; Set accelerations (mm/s^2)

M906 X1800.00 Y2400.00 Z2400.00 U1800.00 E1960.00:500.00 I30 ; Set motor currents (mA) and motor idle factor in per cent

The unmodified print file: JP_talltestPart2.gcode

Short video of unmodified print - https://www.youtube.com/watch?v=3PDYEEwW7_I

First I ran a print of the above file - shown as "F" in pictures below ("F" for front of build plate haha). Printed with HIPS at somewhat high temperatures, no part cooling, 100mm/s. In the FRONT view, the printhead moves left to right along the X axis. In the Right view, the nozzle moves left to right along the Y axis... etc. DAA, PA, etc, all were turned off for the reference print. The reference print is stacked on top of the modified gcode print. For "Fx" I ran the script targeting x f_n, ranging from 5 to 75 across Z=20 (see note above). Yes, the X axis did a good amount of shaking.

Video - https://www.youtube.com/watch?v=6TJ2uW1rX_E
File - x-5-75.gcode

import move

# EXAMPLE CONFIGURATION, PLEASE EDIT BEFORE USING
class motion_parameters:
    dynamic_model = [
        move.spring_damper_parameters(f_n = 0, zeta = 0), # x
        move.spring_damper_parameters(f_n = 0, zeta = 0), # y
        #move.asymmetric_spring_damper_parameters(f_n_negative = 52.5, f_n_positive = 56.9, zeta = 0.02), # y
        move.spring_damper_parameters(f_n = 0, zeta = 0.0), # z
        move.pressure_advance_parameters(k = 0.00)     # e
    ]
    max_speed = 300
    accel = 12000
    jerk = 2000000
    non_motion_max_speed = 300 # i.e. extrusion-only moves
    non_motion_accel = 12000
    non_motion_jerk  = 2000000
    axis_limits = [
        move.axis_limits(speed = 300), # x
        move.axis_limits(speed = 300, accel=500), # y
        move.axis_limits(speed = 22, accel = 1200, jerk = 1000), # z
        None, #e
    ]

# adjust a parameter dynamically based on the z height
def calibration_adjustment(z):
    # example
    value_min = 5
    value_max = 75
    z_max = 20     # mm

    value = z / z_max * (value_max - value_min) + value_min

    #motion_parameters.dynamic_model[0].zeta = value  # adjust x zeta
    #motion_parameters.dynamic_model[1].zeta = value  # adjust y zeta
    motion_parameters.dynamic_model[0].f_n = value   # adjust x f_n
    #motion_parameters.dynamic_model[1].f_n = value   # adjust y f_n
    #motion_parameters.dynamic_model[1].f_n_negative = value   # adjust y f_n
    #motion_parameters.dynamic_model[1].f_n_positive = value   # adjust y f_n
    #motion_parameters.dynamic_model[3].k = value     # adjust pressure advance

# adjust these to adjust the linear interpolation and coarseness of the generated output
# reducing the tolerances will increase the size of the output file (and more likely cause the printer motion planner to choke)
class curve_parameters:
    tolerances = [
        0.002, # x (2µm)
        0.002, # y (2µm)
        0.050, # z (50µm)
        0.100, # e (0.1mm) # low tolerance to prevent pressure advance from adding nodes at the potential detriment of the xy spring-damper control
    ]
    min_dt = 1/200
    
def disable_acceleration_control():
    print('M566 P1') # RRF Jerk Policy 1
    print('M572 D0 S0') #  dis.able pressure advance
    #print('M201 X100000 Y100000 Z100000 E100000') # disable acceleration
    print('M201 X100000 Y100000 E100000') # disable acceleration
    #print('M205 X10000 Y10000 Z10000 E10000') # infinite instantaneous velocity change
    print('M205 X10000 Y10000 E10000') # infinite instantaneous velocity change

def restore_acceleration_control():
    print('M201 X4000 Y4000 Z1200 E3000') # reset acceleration
    #print('M205 X10 Y10 Z10 E10000') # reset instantaneous velocity change
    print('M205 X10 Y10 E10000') # reset instantaneous velocity change

For the image below, same notes - targeted Y axis. I read your warning on going below 20Hz and promptly ignored it hahahahaha

Video - https://www.youtube.com/watch?v=Yc9EpRiLeGE
y-5-75.gcode

import move

# EXAMPLE CONFIGURATION, PLEASE EDIT BEFORE USING
class motion_parameters:
    dynamic_model = [
        move.spring_damper_parameters(f_n = 0, zeta = 0), # x
        move.spring_damper_parameters(f_n = 0, zeta = 0), # y
        #move.asymmetric_spring_damper_parameters(f_n_negative = 52.5, f_n_positive = 56.9, zeta = 0.02), # y
        move.spring_damper_parameters(f_n = 0, zeta = 0.0), # z
        move.pressure_advance_parameters(k = 0.00)     # e
    ]
    max_speed = 300
    accel = 12000
    jerk = 2000000
    non_motion_max_speed = 300 # i.e. extrusion-only moves
    non_motion_accel = 12000
    non_motion_jerk  = 2000000
    axis_limits = [
        move.axis_limits(speed = 300, accel=500), # x
        move.axis_limits(speed = 300), # y
        move.axis_limits(speed = 22, accel = 1200, jerk = 1000), # z
        None, #e
    ]

# adjust a parameter dynamically based on the z height
def calibration_adjustment(z):
    # example
    value_min = 5
    value_max = 75
    z_max = 20     # mm

    value = z / z_max * (value_max - value_min) + value_min

    #motion_parameters.dynamic_model[0].zeta = value  # adjust x zeta
    #motion_parameters.dynamic_model[1].zeta = value  # adjust y zeta
    #motion_parameters.dynamic_model[0].f_n = value   # adjust x f_n
    motion_parameters.dynamic_model[1].f_n = value   # adjust y f_n
    #motion_parameters.dynamic_model[1].f_n_negative = value   # adjust y f_n
    #motion_parameters.dynamic_model[1].f_n_positive = value   # adjust y f_n
    #motion_parameters.dynamic_model[3].k = value     # adjust pressure advance

# adjust these to adjust the linear interpolation and coarseness of the generated output
# reducing the tolerances will increase the size of the output file (and more likely cause the printer motion planner to choke)
class curve_parameters:
    tolerances = [
        0.002, # x (2µm)
        0.002, # y (2µm)
        0.050, # z (50µm)
        0.100, # e (0.1mm) # low tolerance to prevent pressure advance from adding nodes at the potential detriment of the xy spring-damper control
    ]
    min_dt = 1/200
    
def disable_acceleration_control():
    print('M566 P1') # RRF Jerk Policy 1
    print('M572 D0 S0') #  dis.able pressure advance
    #print('M201 X100000 Y100000 Z100000 E100000') # disable acceleration
    print('M201 X100000 Y100000 E100000') # disable acceleration
    #print('M205 X10000 Y10000 Z10000 E10000') # infinite instantaneous velocity change
    print('M205 X10000 Y10000 E10000') # infinite instantaneous velocity change

def restore_acceleration_control():
    print('M201 X4000 Y4000 Z1200 E3000') # reset acceleration
    #print('M205 X10 Y10 Z10 E10000') # reset instantaneous velocity change
    print('M205 X10 Y10 E10000') # reset instantaneous velocity change

Fun to watch and futz with (I did many more prints prior to this), but unfortunately nothing conclusive. What I did do was measure the ringing in the reference print on each side, and then ran the print again only targeting those values (no value hunting). I threw in X=25Hz, and (the reason escapes me now) Y=30Hz. The amplitude of the vibrations are much lower (read: surface is smoother) than the reference print (I also ran a print swapping the X and Y values, where in the inverted prints the results were not as good). Unfortunately the picture doesn't quite paint a clear picture.

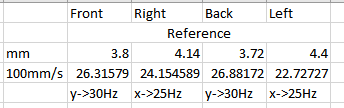
Video - https://www.youtube.com/watch?v=P6JSEvgVD6A
File - x-25-y-30.gcode

import move

# EXAMPLE CONFIGURATION, PLEASE EDIT BEFORE USING
class motion_parameters:
    dynamic_model = [
        move.spring_damper_parameters(f_n = 25, zeta = 0), # x
        move.spring_damper_parameters(f_n = 30, zeta = 0), # y
        #move.asymmetric_spring_damper_parameters(f_n_negative = 52.5, f_n_positive = 56.9, zeta = 0.02), # y
        move.spring_damper_parameters(f_n = 0, zeta = 0.0), # z
        move.pressure_advance_parameters(k = 0.00)     # e
    ]
    max_speed = 300
    accel = 12000
    jerk = 2000000
    non_motion_max_speed = 300 # i.e. extrusion-only moves
    non_motion_accel = 12000
    non_motion_jerk  = 2000000
    axis_limits = [
        move.axis_limits(speed = 300), # x
        move.axis_limits(speed = 300), # y
        move.axis_limits(speed = 22, accel = 1200, jerk = 1000), # z
        None, #e
    ]

# adjust a parameter dynamically based on the z height
def calibration_adjustment(z):
    # example
    value_min = 5
    value_max = 75
    z_max = 20     # mm

    value = z / z_max * (value_max - value_min) + value_min

    #motion_parameters.dynamic_model[0].zeta = value  # adjust x zeta
    #motion_parameters.dynamic_model[1].zeta = value  # adjust y zeta
    #motion_parameters.dynamic_model[0].f_n = value   # adjust x f_n
    #motion_parameters.dynamic_model[1].f_n = value   # adjust y f_n
    #motion_parameters.dynamic_model[1].f_n_negative = value   # adjust y f_n
    #motion_parameters.dynamic_model[1].f_n_positive = value   # adjust y f_n
    #motion_parameters.dynamic_model[3].k = value     # adjust pressure advance

# adjust these to adjust the linear interpolation and coarseness of the generated output
# reducing the tolerances will increase the size of the output file (and more likely cause the printer motion planner to choke)
class curve_parameters:
    tolerances = [
        0.002, # x (2µm)
        0.002, # y (2µm)
        0.050, # z (50µm)
        0.100, # e (0.1mm) # low tolerance to prevent pressure advance from adding nodes at the potential detriment of the xy spring-damper control
    ]
    min_dt = 1/200
    
def disable_acceleration_control():
    print('M566 P1') # RRF Jerk Policy 1
    print('M572 D0 S0') #  dis.able pressure advance
    #print('M201 X100000 Y100000 Z100000 E100000') # disable acceleration
    print('M201 X100000 Y100000 E100000') # disable acceleration
    #print('M205 X10000 Y10000 Z10000 E10000') # infinite instantaneous velocity change
    print('M205 X10000 Y10000 E10000') # infinite instantaneous velocity change

def restore_acceleration_control():
    print('M201 X4000 Y4000 Z1200 E3000') # reset acceleration
    #print('M205 X10 Y10 Z10 E10000') # reset instantaneous velocity change
    print('M205 X10 Y10 E10000') # reset instantaneous velocity change