A Software Solution to Eliminate Ringing?

DigitalVision

Thanks for the encouraging comments.

@zemlin said in A Software Solution to Eliminate Ringing?:

The low-frequency ringing I get I believe is mechanical due to the flex in the rods - if I understand your concept, it might be able to compensate for the resonant frequency of my gantry rods, or at least partially. On my printer the flex is going to be worse at the center and lesson as an axis approaches the rod support at the ends.

I'm personally pretty thrilled that a simple 1-parameter linear spring model had such a big impact in my test, but you are right – if the dominating source of spring in your system is a flexing rod, then the spring constant is going to be position dependent. It's probably pretty doable to build a slightly more complex model and calibrate that out though. An even more complex motion would be a delta printer where the both the end-effector position relative to the towers matters and probably also the carrier positions along the verticals.

@sebkritikel said in A Software Solution to Eliminate Ringing?:

I enjoy the Duet and RRF ecosystem, but strongly desire improvements in DAA/Input Shaping/ringing reduction (independent X and Y tuning... even reducing artifacts from Z axis movements (depending on printer build)...).

Agreed. Luckily, it's pretty easy to treat the axes mostly independently with this technique, at least for a cartesian printer.

@tgarr said in A Software Solution to Eliminate Ringing?:

I guess I'd assumed the right place for this kind of compensation is really in the firmware, but we already push so many machine specific tweaks regarding temperature, retractions, etc into the G-code maybe it wouldn't be so bad to have this in the slicer.

Unfortunately, with this simple geometry I'm already pushing the limits for the motion planer look-ahead. A single corner in the example above is turns into ~20 lines of G-code. The good news is that a firmware implementation should actually be pretty simple (ignoring the s-curve aspect): The motion planning would be independent of this compensation approach – the compensation would only need to happen at the very end and in-line with the motion control.

Adamfilip

Awesome, looking forward to hearing @dc42 thoughts on this.

theruttmeister

@DigitalVision said in A Software Solution to Eliminate Ringing?:

Thanks for the encouraging comments.

@zemlin said in A Software Solution to Eliminate Ringing?:

The low-frequency ringing I get I believe is mechanical due to the flex in the rods - if I understand your concept, it might be able to compensate for the resonant frequency of my gantry rods, or at least partially. On my printer the flex is going to be worse at the center and lesson as an axis approaches the rod support at the ends.

I'm personally pretty thrilled that a simple 1-parameter linear spring model had such a big impact in my test, but you are right – if the dominating source of spring in your system is a flexing rod, then the spring constant is going to be position dependent. It's probably pretty doable to build a slightly more complex model and calibrate that out though. An even more complex motion would be a delta printer where the both the end-effector position relative to the towers matters and probably also the carrier positions along the verticals.

I suspect that because most delta's are symmetrical, a single spring model is going to be close enough. I would expect asymmetrical delta's to be different.

@sebkritikel said in A Software Solution to Eliminate Ringing?:

I enjoy the Duet and RRF ecosystem, but strongly desire improvements in DAA/Input Shaping/ringing reduction (independent X and Y tuning... even reducing artifacts from Z axis movements (depending on printer build)...).

Agreed. Luckily, it's pretty easy to treat the axes mostly independently with this technique, at least for a cartesian printer.

@tgarr said in A Software Solution to Eliminate Ringing?:

I guess I'd assumed the right place for this kind of compensation is really in the firmware, but we already push so many machine specific tweaks regarding temperature, retractions, etc into the G-code maybe it wouldn't be so bad to have this in the slicer.

Unfortunately, with this simple geometry I'm already pushing the limits for the motion planer look-ahead. A single corner in the example above is turns into ~20 lines of G-code. The good news is that a firmware implementation should actually be pretty simple (ignoring the s-curve aspect): The motion planning would be independent of this compensation approach – the compensation would only need to happen at the very end and in-line with the motion control.

True machine compensation (like bed leveling) should always be at the machine level.

This is excellent work. And I'm actually curious just how far this could go... just how flexible a machine could you get away with!?

tgarr

@theruttmeister said in A Software Solution to Eliminate Ringing?:

This is excellent work. And I'm actually curious just how far this could go... just how flexible a machine could you get away with!?

I suppose this could do wonders for a "hangprinter"?

theruttmeister

@tgarr probably!

Although, going to steel tape instead of wire or rope would get you fairly dramatic stiffness.

A Former User

@theruttmeister said in A Software Solution to Eliminate Ringing?:

@tgarr probably!

Although, going to steel tape instead of wire or rope would get you fairly dramatic stiffness.

@tgarr
when considering a "wire"/rope that has low stretch, e.g. dyneema rope from a local fishing, sailing, climing, etc. shop seems to be very good on pull compared to its weight (of course nowadays rather online)

DigitalVision

@tgarr said in A Software Solution to Eliminate Ringing?:

I suppose this could do wonders for a "hangprinter"?

That's an interesting thought. Model-based spring/acceleration control seems like a great fit there. You can discard the damping term, since air resistance is likely negligible. You are left with four forces – the gravity pulling down and the three lines that now are treated as springs. The gravity force can simply be turned into an offset to the acceleration, so you get a simple system of equations to solve for d1, d2, d3 to give the end effector the desired target acceleration.

For lines, I would think that rather than maximizing stiffness you want to focus on lines that provide a simple well-defined spring function so you can leverage the spring to create the desired target force with high precision. (Or maybe stiff lines with the addition of physical springs would work best). Obviously you don't want them to be too elastic since that will limit the speed by which you can change the tension (the end-effector jerk). Braided lines/ropes are probably not great since I suspect they have a lot of internal friction in them as they stretch damping any pure spring behavior.

DigitalVision

@Adamfilip said in A Software Solution to Eliminate Ringing?:

Awesome, looking forward to hearing @dc42 thoughts on this.

Me too. Funny – I just went back to a >2 year old post of mine here and found this comment by @dc42:

My thinking is this. Let's assume a Cartesian printer for now. In order to accelerate (say) the X axis, the motor and belt have to impart a force to the head given by F=ma. But the belt and the motor are springy, so in order to really impart force F to the mass of the print carriage, the motor must move by an additional amount S=ma/k where k is the spring constant. If the acceleration changes abruptly, then this requires instantaneous changes in motor position, which are impossible; but if we use S-curve acceleration then the required changes in motor position are gradual and should be achievable.

I never really registered that back then (I was focused on figuring out why my extruder wasn't behaving according to theory), but this must have planted a seed in my subconsciousness.

So, with this serving as a kind of proof of concept I'd love to hear dc42's thoughts on this:

Replacing "instantaneous velocity change" with a simple smoothing pre-processor that replaces sharp corners with small arc segments (G2/G3) controlled by a smoothness parameter (e.g. G187). There are plenty of options here with e.g. an angle criterium to heuristically identify curve approximations vs sharp corners, but a simple 'max deviation' should probably suffice initially. Ideally you want to implement a transition curve rather than a simple arc to keep the acceleration continuous, but continuous velocity with an approximate correction may be sufficient initially. The arc approach could be prototyped as a simple offline pre-processor at first.
Approximating the spring-damper-correction without s-curves as the simulation seems to indicate could work.
The effort/plan to implement true s-curve motion control. This seems like the inevitable end-state.

A Former User

@DigitalVision
Wow - would be great to have this optional sometime in the future! Would be great to have beside the option to calculate the val the "old" try-n-error option to print a tower with diffrent "zeta"-val...

Have you been aware of this project I just read about today (?): https://www.ulendo.io (which seems to do for the avarage-joe what create-it-real does for OEMs since years)

Just exploring all this for me new stuff, I stumbled across "Helling-Bestehorn" (the "smooth-runner") and "Polynom of the 5th order" which seems to be an "allrounder" in terms of motion-control - would really like to hear your opinion on it...

Congrats & Cheers & all of it

DigitalVision

@LB said in A Software Solution to Eliminate Ringing?:

@DigitalVision
Wow - would be great to have this optional sometime in the future! Would be great to have beside the option to calculate the val the "old" try-n-error option to print a tower with diffrent "zeta"-val...

Thanks. Calibrating the f_n is actually really easy using a similar approach to my proposed method of calibrating pressure advance. You print a simple test print varying the f_n parameter layer-by-layer. You will see a very clear phase inversion in the ringing pattern at the point that corresponds to the right f_n number and you can simply measure the height of that inversion to find the right value. That's how I determined the f_n = 40.4 Hz value above. A less accurate / coarse method is to measure the ringing spacing (peak-to-peak) at known print speed. In this case, 80 mm/s print speed, 40 Hz natural frequency corresponds to 2mm peak-to-peak spacing.

Just exploring all this for me new stuff, I stumbled across "Helling-Bestehorn" (the "smooth-runner") and "Polynom of the 5th order" which seems to be an "allrounder" in terms of motion-control - would really like to hear your opinion on it...

I've not heard about Helling-Bestehorn – seems like a sinusoidal interpolation basis function. For smooth interpolants that satisfy a continuous curvature constraint (e.g. continuous centrifugal force) a 5th order polynomial is the most straightforward choice. You have 6 coefficients that you solve by 6 constraints: at each end you fix the position, velocity and curvature and you get a simple closed form solution for the polynomial coefficients. I've looked at this to smooth tessellated paths into a continuous curve.

A Former User

@DigitalVision said in A Software Solution to Eliminate Ringing?:

@LB said in A Software Solution to Eliminate Ringing?:

@DigitalVision
Wow - would be great to have this optional sometime in the future! Would be great to have beside the option to calculate the val the "old" try-n-error option to print a tower with diffrent "zeta"-val...

Thanks. Calibrating the f_n is actually really easy using a similar approach to my proposed method of calibrating pressure advance. You print a simple test print varying the f_n parameter layer-by-layer. You will see a very clear phase inversion in the ringing pattern at the point that corresponds to the right f_n number and you can simply measure the height of that inversion to find the right value. That's how I determined the f_n = 40.4 Hz value above. A less accurate / coarse method is to measure the ringing spacing (peak-to-peak) at known print speed. In this case, 80 mm/s print speed, 40 Hz natural frequency corresponds to 2mm peak-to-peak spacing.

Ah! I have really problems with a big printer I build a while ago with ca. 1x1meter with "springiness" of the belts and axis because of ca. 5kg mass (but it has less then 0.01mm bending by gravity in the middle...) in x & y, so that the max. jerk setting ist pretty low for now, and this could help I guess to be able to make it faster all round without wobbling/ringing one day! Would be great if the z-axis is taken out of the equation in a first aproache and just have x&y separate, since on most cartesian printers those are unequal from the buildup.
So if you can tell me how to support you I try my best, e.g. I can offer bavarian beer or you open a patreon-page or similar?

Just exploring all this for me new stuff, I stumbled across "Helling-Bestehorn" (the "smooth-runner") and "Polynom of the 5th order" which seems to be an "allrounder" in terms of motion-control - would really like to hear your opinion on it...

I've not heard about Helling-Bestehorn – seems like a sinusoidal interpolation basis function. For smooth interpolants that satisfy a continuous curvature constraint (e.g. continuous centrifugal force) a 5th order polynomial is the most straightforward choice. You have 6 coefficients that you solve by 6 constraints: at each end you fix the position, velocity and curvature and you get a simple closed form solution for the polynomial coefficients. I've looked at this to smooth tessellated paths into a continuous curve.

Ah - have to dig deeper one day I guess - currently over the top for me - thanks anyway for now!

DigitalVision

If this method will turn out to be useful, here’s what I think the likely end-state (at least as far as I can see) is for 3D printer motion control.

To replace instantaneous velocity change to handle segmented curves in a continuous motion, it is likely that we need a way of defining smooth (G2 continuous) profiles. Using some type of spline representation is probably the best choice, and out of the different representations NURBS is the most obvious one, since it has a number of good properties like the ability represent conics (like circular arcs) exactly. We can certainly get away with something slightly simpler than NURBS, but the difference in complexity is hardly significant.

Afaik, there is no good spline representation that has a straightforward arc-length parametrization though, something we need to effectively generate physical motion profiles (and achieve C2 continuity). The best path is probably to create a re-parametrization through a second approximating spline (approximating the inverse of the arc-length function).

With this we can generalize the current motion primitives (line segments, arcs), support transition curves and other smoothing primitives including the ability to represent (and possibly reconstruct) the original curved surfaces that were used to generate tessellated polygonal/STL representations.

With S-curve motion, acceleration planning would be the job of defining (at a minimum) a piecewise linear acceleration profile over the arc-length parameter ensuring adherence to all motion limits. Higher orders than 3 may be valuable to model more complex compounded spring-damper systems, but lacking any proof of that a 3rd order model seems right.

So we get effectively 4 functions:

From the motion planner, we get a (at minimum piecewise-linear and continuous) function a(t), that when doubly integrated gives a mapping s(t) from time t to arc length s.
From the inverse arc-length-approximating spline, we get another mapping q(s) from s to the NURBS parameter q.
From the NURBS profile we get the mapping from q to the spatial dimensions {x,y,z,e,…}
From the spatial dimensions we apply model-based control (spring-damper correction) and machine configuration to get final actuator axes positions.

A somewhat complicating factor is that I believe today there is a tight coupling from 4 back to 1. Motion constraints defined in actuator space feed back to the motion planner. With today’s simple motion primitives these constraints can probably be expressed in closed form with respect to the acceleration profile, but I don’t think that’s going to be easy or even possible with the above scheme. One option (a) is to decouple this by providing (or calculating) sufficient guard-rails to the spatial constraints for the motion planner that machine constraints don’t need to be considered. Another option (b) is an iterative process feeding back e.g. Taylor-approximations of the constraint mappings.

The nice thing about option a is that it simplifies the implementation significantly, and with some limitations even allows 1-3 to be computed offline. That’s effectively what I did above but with a much simpler geometric profile. I also included the model parameters for the spring compensation though, which unfortunately makes the output incompatible with the model-based control RRF already does for extruder pressure advance, so I had to disable that.

For prototyping I can fairly easily hack 1-3 together, creating a time-parametrized motion profile. I wonder how to best feed that to RRF is though. Since RRF supports constant acceleration segments already, they’d be great candidates to approximate the profile. I.e. pairs of M204 (acceleration limit) and G1 commands to describe the path. For this to work with high segment rates, I’d probably need to hack the firmware a little bit to bypass the motion planner and instead have it follow the provided motion profile exactly, although I’d love to hear if there are better options.

dc42

What I have in mind is that when the GCode involves a change in direction between adjacent printing moves, RRF will insert a joining move between them. This joining move would be a quadratic or cubic in shape, and would deviate from the path specified in the GCode by no more than a user-set deviation parameter. So an internal corner would be cut by no more than this amount. Different motors would be executing trajectories of different shapes during this joining move.

bot

@dc42 @DigitalVision

Why don't we use an approach that has already been implemented and proven in Klipper firmware? It sounds similar.

Described here: https://onehossshay.wordpress.com/2011/09/24/improving_grbl_cornering_algorithm/

First let’s assume that at a junction of two line segments, we only look at centripetal acceleration to simply things. In other words, we assume the tangential velocity is zero and the velocity through it is constant. At the junction, let’s place a circle with a radius R such that both lines are tangent to the circle. The circular segment joining the lines represents the path for constant centripetal acceleration: junction = sqrt (a max R) [See URL for correct forumlas]. Where the maximum junction velocity v junction is the fastest speed the CNC can go through the junction without exceeding the CNC’s maximum allowable acceleration a max.

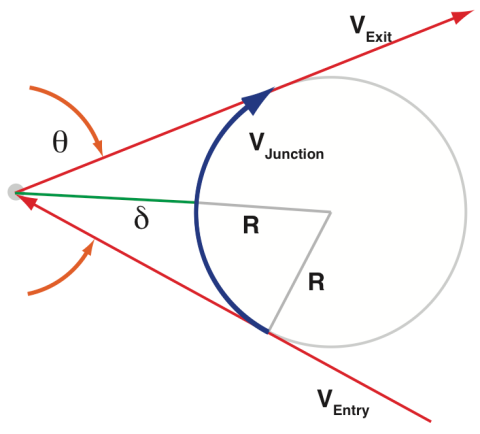
This circular segment creates a virtual deviation from the path delta, which is defined as the distance from the junction to the edge of the circular segment. This delta parameter is defined by the user as a setting, which indirectly sets the radius of the circle, and hence limits the junction velocity by the centripetal acceleration. Think of the this as widening a race track. If a race car is driving on a track only as wide as a car, it’ll have to slow down almost to a complete stop to turn corners. If we widen the track a bit, the car can start to use the track to go into the turn. The wider it is, the faster through the corner it can go.

A note on the Klipper implementation:

However, in Klipper, junction speeds are configured by specifying the desired speed that a 90° corner should have (the “square corner velocity”), and the junction speeds for other angles are derived from that.

More info on the Klipper firmware: https://www.klipper3d.org/Kinematics.html

DigitalVision

@bot said in A Software Solution to Eliminate Ringing?:

@dc42 @DigitalVision

Why don't we use an approach that has already been implemented and proven in Klipper firmware? It sounds similar.

This approach is certainly the easiest one, especially in a firmware that already supports arcs, but the problem is that this method doesn't preserve a continuous curvature. There is an abrupt change in curvature going from the smooth line to the circle, something that would yield an instantaneous position change with spring-damper compensation.

In road and railroad construction you never build curves like that for the same reason. You would have to turn your steering wheel instantaneously to a new position to follow such a path. What civil engineers do instead is add a transition curve (a spiral shape) that creates a gradual increase in curvature.

With a polynomial spline (like @dc42 suggests) we can create a curve that has a gradual curvature.

bot

@DigitalVision interesting. Thanks for the explanation.

That makes sense. Instead of the G1 curvature, it might be G2 or G3?

I'm not as smart as you two when it comes to these algorithms, so I'll keep to myself now. I just get worried when there is talk of the firmware injecting intentional deviation into the stream. I'll have to wait and see results, I guess!

[Edit: Just to clarify, the Klipper method does not actually deviate from the path -- it is only a virtual deviation to calculate the speed change possible.]

DigitalVision

@dc42 said in A Software Solution to Eliminate Ringing?:

What I have in mind is that when the GCode involves a change in direction between adjacent printing moves, RRF will insert a joining move between them. This joining move would be a quadratic or cubic in shape, and would deviate from the path specified in the GCode by no more than a user-set deviation parameter. So an internal corner would be cut by no more than this amount. Different motors would be executing trajectories of different shapes during this joining move.

In order to satisfy a smooth curvature (G2 continuity) at both the start end end of such a joining segment, I you either need a higher order polynomial than quadratic or cubic or you need to piecewise combine multiple polynomials. An easy way to think about it is that a cubic polynomial only has one point where the second derivative is zero and you need two. For a single polynomial to describe a symmetric transition curve, I think you need a 4th degree (quartic) polynomial, and for a generic transition between two arbitrary points the degree increases to 5 (quintic?).

Another important property that we want for a smoothing method is to allow for constant arc-length speed. I.e. the print head should be able to move through a circle made up of line segments at constant extrusion speed. This means that ideally you want the curve to be parametrized based on arc length. For a circular arc this is trivial, but it's not so easy for a polynomial curve shape. That's the reason I suggested a second inverse-arc-length approximating polynomial.

In the extension though, if you implement say a spline of 3rd order polynomials to support joining moves you've basically done 90 % of the job of supporting a general spline motion profile. And going all the way has some very nice properties. The slicer could now output perfect arc and elliptical shapes, and replicate more generic curve shapes out of most CAD software perfectly. I believe this is where the industry is going for advanced CNC control paths.

DigitalVision

@bot said in A Software Solution to Eliminate Ringing?:

@DigitalVision interesting. Thanks for the explanation.

That makes sense. Instead of the G1 curvature, it might be G2 or G3?

That's right. In the end, we actually need C2 continuity, but if you start with G2 you can reparametrize it to achieve C2.

I'm not as smart as you two when it comes to these algorithms, so I'll keep to myself now. I just get worried when there is talk of the firmware injecting intentional deviation into the stream. I'll have to wait and see results, I guess!

You bring up some good questions. The intentional deviation may sound controversial, but it's actually the reality already. I don't know of any high-end professional CNC machine that doesn't do this (since it significantly increases the motion speed), and that's generally an application with much tighter tolerance requirements. In the case of joining line segments and doing spring-damper compensation the outcome is actually a more faithful reconstruction of the original curve.

You could make a valid argument that the smoothing should be done by the slicer instead of the firmware. I don't have a strong opinion either way. I think the reality is that a lot of the way our current pipelines are constructed just kind of happened and making a local change is much easier than driving a change across softwares. For example there is no good reason a slicer should need to know what your filament diameter is.

If smoothing were implemented in firmware, I would expect it to be controlled by a cordial error tolerance parameter that you could set to zero to disable the behavior.

[Edit: Just to clarify, the Klipper method does not actually deviate from the path -- it is only a virtual deviation to calculate the speed change possible.]

Thanks, that makes sense.

bot

I've been modifying PrusaSlicer for the past few months as a way to slowly learn and get used to how it works under the hood. My end goal is to make sure the slicer and firmware are playing nicely together. If you want to try and put some of this smart stuff into PrusaSlicer, maybe just for testing, I'd be glad to lend a hand with the tedious bits or pointing you around the codebase as best as I can.

I do get worried at the thought of the firmware having more calculation overhead. Once we solve the "jerk" problem, and we can round corners faster, then we solve the ringing problem, we'll quickly encounter the next problem: too many segments too fast.

CCS86

Great thread!

I am very interested to see this progress.