S-Curve/ sinusoidal , Jerk +acceleration

[vp]

3. How to utilize the cancellation points ?
From the Fourier transform we know, we could have no ringing after (that doesn't mean not in between) a speed change. To be able to use the zero amplitude positions to cancel the total ringing of a complete speed change, we have to know the period time which is 2 * pi/sqrt(c/m). Unfortunately c/m is by far not constant and not only one c/m has to dominate. It will vary among different fdm printers by a factor of up to 100 and it will vary also during a print. E.g. on a prusa style printer with a moving bed, the mass as well as the stiffness changes significantly. For the 1st layer c/m is big and for the last layer e.g. 200 mm above the bed with 500 g printed c/m will be very small, depending on the shape of the print, it might vary arbitrarily. On ultimaker style printer the same is valid, in a corner the stiffness is max and in the middle min. If the stepper current is doubled, c/m of the stepper is doubled. If the current of the stepper drops at high velocities, c/m of the stepper follows.... so c/m is not constant and in addition there is more than 1 mass spring damper system acting !

So in total the length of a speed change would have to be adjusted during the print - to hunt the cancelation points. I don´t claim that this couldn´t be done (in theory), but for e.g prusa printers it won´t be doable or only in certain cases. On ultimaker style printers it will "only" work near e.g. the middle of the bed and as long the stepper current doesnt drop to much due to speed.

In my case my stiff printer has (stepper, belts and tubes) c/m values in the range of 1e5 to 1e6 [N * kg/m]. My slow printer has c/m values about 1e3 to 1e4 [N * kg/m].

A c/m of 1e6 gives a period time T of 2 * pi/sqrt(1e6) = 63ms (or 160 Hz); a c/m of 1e3 gives 199 ms or 5 Hz.
My stiff printer uses printing accelerations > 1g, so in 63 ms the speed change after one period time T of acceleration is > 10.000 * 0.063 = 630 mm/s. With 0.2 g at my slow printer the speed change would be 2000 * 0.2 = 400 mm/s. In other words the nowadays used acceleration settings just "mirrow" c/m and the time used for acceleration when printing is between 0 and << 0.1 - 0.2 * T. The fourier transform doesn´t show a significant difference there between different moveplan profiles - but the amplitudes of the waves generated during the move differ.

So if we would print using speeds like before, we would have to reduce the acceleration to catch the 1st wave cancelation point at 1 * T. Increasing the acceleration time will amplify extrusion problems. In addition i don´t want to print slower....

If we would hunt for the 1st wave cancelation point by increasing the max speed, we would get really high speeds, with the need for "max. acceleration as a function of speed" and a working pressure advance.

In case we ask for multiple speed changes (moveplan) and not for a single speed change, the cancelation possibility gets more interesting. Multiple speed changes in a row can stimulate much lower frequencies as a single speed change. So we know that normally a single speed change operates at e.g. << 0.2 T. But multiple speed changes together could easily stimulate at or above 1 T. The high level move planner would have to adjust the move plan in a way, that the speed changes itself act close to the cancelation points. This could be beneficial for a lot of small moves in a row. E.g. when printing top and bottom layers and it fills a gap by zigzag moves.

4. Is a triangular profile a good choice to compare s-curve acceleration with a rectangular change ?
In addition to above, yes and no. It is true that one can blend the fourier transform from a triangle over a trapezoid into a rectangle (see the figure below). But whos says that we have to limit it to that simple kind of shapes ?

Just try the following: instead of one triangular shape apply 2 after each other. Both have the half width of the single one and same amplitude. By that the frequency spectrum is shifted to the left by T/2 and the 1st wave cancelation is also at 1 * T, like in the rectangular case (and not like 2 * T in the single triangular case). So comparing a triangular with a rectangular profile just compares two profiles and not all available possibilities.

5. The main fdm problem is extrusion - not ringing.
Ringing can be solved by proper engineering. Extrusion is thermodynamically and fluid wise limited - these limits "cannot" be changed - at least not much. Pressure advance would help a lot, if it would have a chance to work. With a stepwise acceleration change, it can only work under certain limiting conditions. With “s-curve” (a more gentle) acceleration the pressure advance jerk problem caused by the step wise acceleration change would be "wiped away". Pressure advance could show its potential.

6. Because one picture says more than 1000 words, i have attached some figs for a system like m * xdotdot +c * x = c * y(t) (so no damping and only one spring mass system). m = c = 1.

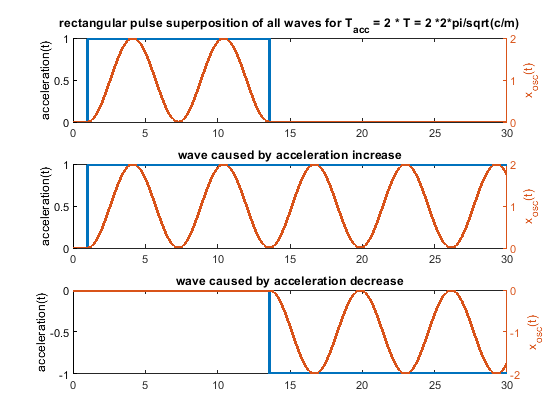
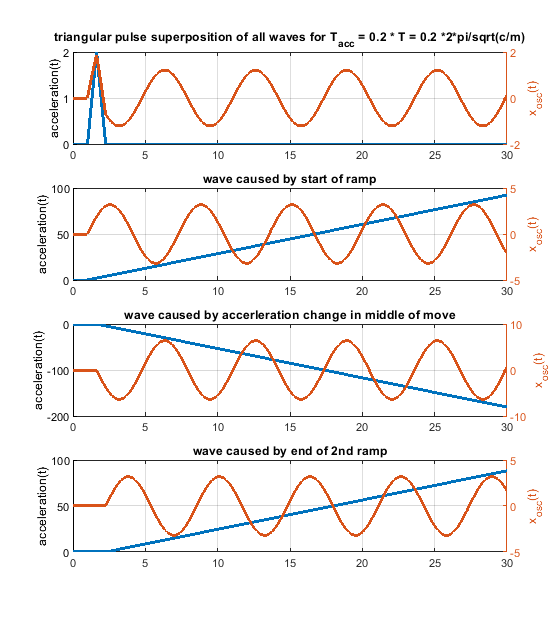
In case the acceleration time equals to the time period T, as shown in the fourier transform, the whole rectangular acceleration change produces no remaining waves (only without damping, with damping like in real life this doesn´t work perfectly at all). The triangular as well as trapezoidal acceleration change show waves - which would be damped quickly including damping, but this is the ringing we see on pure x/y/z printers.

Blue is the acceleration change ydotdot(t), orange is only the oscillation part of x(t).

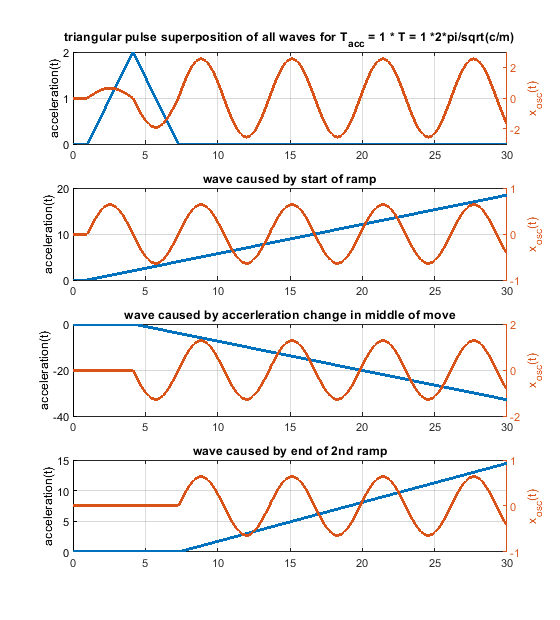
Same for acceleration time equals to the time period T * 2 - now the triangluar change also produces no remaining waves. If instead of one triangle of width "a" 2 triangles of width "a/2" and the same height would be applied, the triangular profiless also would also show no remaining waves at 1 * T - like the rectangular case.

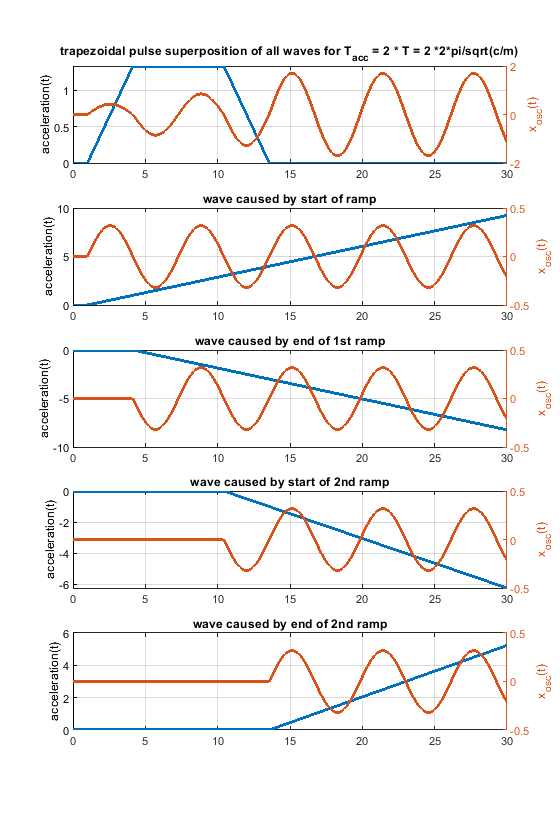
The same for a pulse width of 0.2 T. In real life it looks much better, because damping acts.

[stewwy]

Just my 2 pence worth, reading this thread it is going to be of great benefit to some but make no difference to others.

From a practical perceptive it would be most useful to have S-curve available under an M-code, it could then be used per print.

I've used it on my Cartesian before I got my Duet (using Marlin2 and an MKS-Sbase) it does allow me to print faster at the same quality, Plus my desk didn't vibrate as much

However it did have those awful stepper drivers, so theres that.

[T3P3Tony]

@stewwy the option to select which acceleration type is used is part of the plan.

[Hardware_SortingRobotics]

When S-curve acceleration is applied will the curve look more like this picture instead of a trapezoid? I got the picture off of the prusa calculator website.

[dc42]

That picture doesn't illustrate S-curve acceleration.

[stewwy]

Is this what is trying to be achieved?

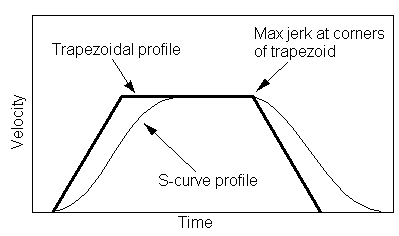
If so, do we also need to think about the timing ? As it effectively moves the area under graph in a positive way which is going to lead to an overrun. or am I over-thinking this?

Apologies if this has already been discussed, I didn't notice it on a quick re-read of the thread.

[dc42]

The problem with changing the profile like that is that it makes the total acceleration and deceleration times longer, which slows the print down. You could keep the trapezoidal profile but reduce acceleration and deceleration to lengthen the acceleration and deceleration phases instead, and that too would typically reduce ringing.

To get an accurate comparison, you need to use a higher peak acceleration in the S-curve profile than you do in the trapezoidal profile, so that the total acceleration time is the the same in both cases. Similarly for deceleration.

[markdashabout]

Did you say higher pint speeds?

[stewwy]

@dc42 makes sense, heading towards the classic bell shaped curve, if you had unlimited speed and limited acceleration that is where you would want to be anyway.

[JoergS5]

just for info: I saw the TMC5161 uses S-Shaped motion. I'll test whether it reduces vibrations at the extruder.

[Neonode]

I am using printer with ball screws and I can say that for me S-curve is really important. While belt motion got some elasticity ball screw got 0. This is really cool as I have no ringing at all and really smooth print but I need to live with very low Jerk and acceleration settings like 200 Jerk and 300 acceleration. If I got faster the ball screws start producing noise like hammering during direction change. Current jerk implementation is just stupid. It is okay to change the speed with jerk but it is not okay to change the direction with half of the jerk speed. So I am really waiting for S-curve to come as it really will make my system to perform really well and to be silent.

[Catalin_RO]

@neonode What size of ball screws are you using (length, diameter and pitch) and what size of stepper (NEMA* and the torque)?

[Edgars Batna]

@dc42 said in S-Curve/ sinusoidal , Jerk +acceleration:

Unfortunately, in 3D printing we have a much worse problem, which is that curves are approximated by straight lines. This unfortunately forces us into making the first derivative of position discontinuous, to avoid dropping the speed to zero at every boundary between line segments in a curve. As long as we are forced to do this, there is very little point in worrying about the discontinuity of the second derivative.

If we ever reach the situation where the model files we slice represent curves properly, and the slicers that generate gcode from them generate Bezier curves, cubic splines or some other representation of curves, then implementing smooth changes in acceleration may be worth looking into.

Yes, but that would also mean whole new generation of modelling tools, gcode, slicers - generally the whole toolset. Can't we have a feature which approximates segmented movement using curves? Supporting curves way down the pipeline in the firmware is a thing that can be reused once the slicers are up to par.

The thing about curves is that nothing is a 100% curve. The 3d models are meshes or a mix of corners and curves that would otherwise need to be approximated somewhere, be it in firmware (if hardware permits) or PC application software as a pre-processing step.

[Urban]

@neonode I agree!! The line segment jumps can be handled with filtering in the servo driver even if that is not a perfect solution.

[gnydick]

I agree with trying out s-curve. My printer is turning out great, and I want higher speed printing.

These ripples are more visible than they are palpable, but the corner ringing is detectable to the touch.

https://dyzedesign.com/2016/10/printing-300-mm-s-part-1-basics-hardware/

https://www.controleng.ca/servosoft/SSHelp1033/source/MotionProfile.htm

I'm making another post with the photo with a different topic, keep an eye out

[dc42]

Have you looked at the dynamic acceleration control feature in RRF 2.02RC6? It may help you to control the ringing. See https://duet3d.dozuki.com/Wiki/Gcode?revisionid=HEAD#Section_M593_Configure_Dynamic_Acceleration_Adjustment.

[gnydick]

@dc42 worth a try. Still would like s-curve. I'm not too worried about being slightly slower, my printer is printing cleanly at 150mm/sec, probably could go faster if I had a more powerful system of drivers and motors.

[Twigz]

Good morning

I've run into a problem that may or may not need a s curve.

I'm driving the x and y gantry with a brushless/ encoder + lead screw setup and am able to get speeds up to 1mtr/s.

The whole hotend assembly is rather hefty at 0.5 kg. At quick direction changes (corners of Infill at 45 degrees in a cube) it shakes uncomfortably much and I have to reduce to 500mm/s^2. At this acceleration it would take 1.5 seconds and approximately 500mm to get to its maximum speed.

I did some tests and when printing a corner in a radius of 75mm an acceleration of 10.000mm/S^2 even seems reasonable
My thought would be that the slower ramping up is what is causing this improvement. (as the direction turns from x to y the y gantry has to move exponentially faster)

At 10.000mm/s^2 it only takes 0.07 second and 25mm to get to its maximum.
If we interpolate between the two that gives 0.75 seconds and 262mm to obtain maximum speed. (in reality this would only be 25% quicker) this could decrease the overall print time on long complicated prints by quite a lot.

I think printers with either a high capability of speed or a heavy hotend assembly will greatly benefit from a ramping acceleration/deceleration.

I don't know if this is easier to setup than a s curve but perhaps it would be an idea to multiply the acceleration by time and by a factor in time to reach the max acceleration.
In this case we could ramp up to 10.000mm/s^2 in 1 second and it would look like this:

Acceleration = (acceleration*((t/factor) ^2))

After 0.1 seconds:
Acceleration= (10.000*((0.1/1) ^2)=100mm/s^2

After 0.5 seconds:
Acceleration=(10.000*((0.5/1) ^2)=2500mm/s^2

After 0.75 seconds:
Acceleration=(10.000*((0.75/1) ^2)=5625mm/s^2

After 1.0 seconds:
Acceleration=(10.000*((1.0/1) ^2)=10.000mm/s^2

Ramping up to 5000mm/s2 in 3 seconds:

After 1 seconds:
Acceleration= (5000*((1/3) ^2)=555mm/s^2

After 2 seconds:
Acceleration=(5000*((2/3) ^2)=2222mm/s^2

After 2.5 seconds:
Acceleration =(5000*((2.5/3)^2)=3472mm/s^2

After 3 seconds:
Acceleration=(5000*((3/3) ^2)=5000mm/s^2

Applying the same formula to the extruder would also ramp the extruder to not create under or over extrution during the ramping up.

I've never heard of issues caused by the jerk between acceleration and max speed so this may or may not be a problem.

Keeping acceleration and deceleration seperate would lead to even more tuneability as acceleration tends to be able to be a little bit higher.

Jeff

[Twigz]

After some more calculations and thinking i figured the reverse might be beneficial as a replacement for jerk. To stop extreme shaking and ringing the best would be to get to a full stop before changing direction.
In this case reversing the above formula to jerk=jerk*(SQRT(T/Factor)) would start from a stop with a high acceleration where the acceleration increases exponentionally less.

You could then finetune the jerk for sharp corners and direction changes after which you can tune the acceleration to the max your printer is capable off.

I made some Ghraps to show what i mean in the hopes of it making things more clear in my explanation.

EDIT: When the jerk speed has been reached it would continue using acceleration instead.

jeff

[dc42]

What I am looking to do at the same time as implementing S-curve acceleration is to replace jerk by junction deviation, but for the deviation to be planned instead of mythical. This will make it possible to eliminate attempts to change the speed of the motor instantaneously. In fact i see little point in implementing S-curve acceleration without tackling jerk (i.e. commands to change motor speed instantaneously) at the same time, because instantaneous speed change is much worse than instantaneous acceleration change.

When implementing S-curve acceleration, you can either keep the peak acceleration constant (which lengthens the acceleration time, and hence printing time), or you can increase the peak acceleration so as to keep the acceleration time constant. Lengthening the acceleration term in itself reduces ringing in most cases. So where S-curve acceleration has been reported to improve print quality, it may actually be the increased acceleration time that is making the difference. Also, the Bezier curve implementation of S-curve acceleration in Marlin has the side effect of reducing average acceleration when the acceleration takes place over several short segments, for example when printing curves.

I do expect S-curve acceleration to improve the sound of the printer when cornering; although I think there are probably easier ways to do that.