A Software Solution to Eliminate Ringing?

[DigitalVision]

@DigitalVision said in A Software Solution to Eliminate Ringing?:

Assuming 500g of extruder weight we get f_n = sqrt(71.5 * 1000 / 0.500) / (2*π) = 60.2 Hz. That's remarkably close to the 60.5 Hz number I got from tuning.

One thing that's been bugging me about this calculation is that I'm leaving out the counter-spring from the opposing belt. I initially thought that spring force wouldn't matter since that side would be slacking. But would it really?

If we model the belt like a spring like this:

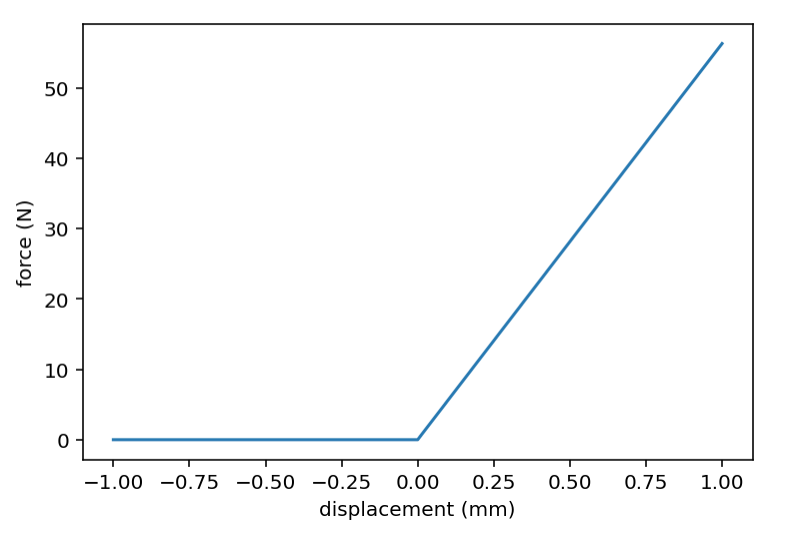
And then add a counter spring and apply some tension to the belt we get the following two forces:

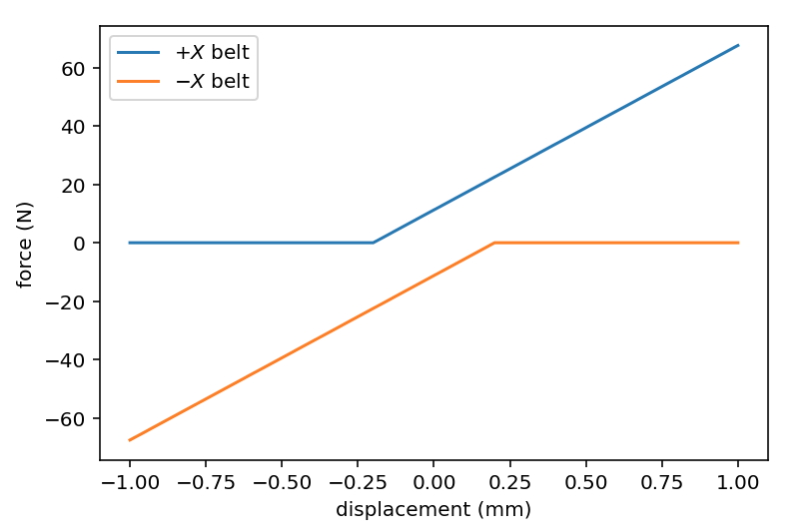
Summing these two, we should expect a net spring function like this:

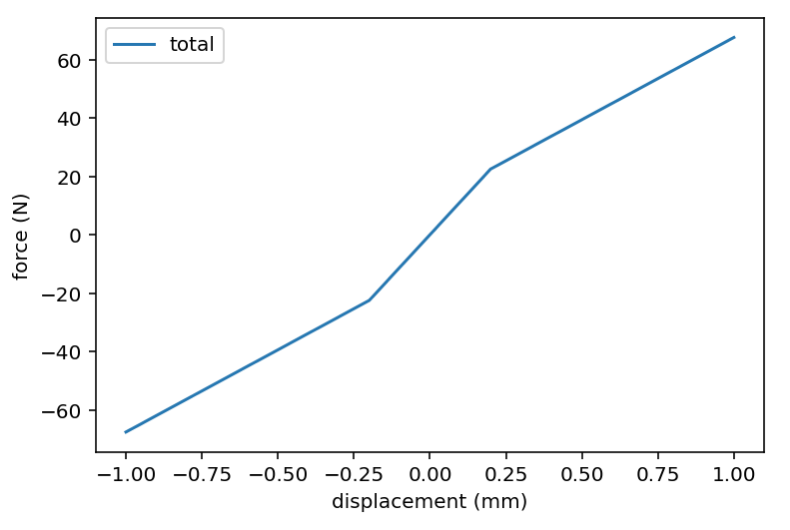
Note that the slope in the center region is twice that from my calculation above, and only beyond the cutoff point (when it exceeds the pre-tension) will the opposing end of the belt slack. So we should in theory expect a sqrt(2) ≈ 1.41 higher ringing frequency than I calculated. I.e. 85 Hz vs 60 Hz. Since I’m not getting that something is off. I can come up with three hypotheses:

1. The acceleration exceeds the belt tension causing the opposing belt to slack. This would mean that we operate in the 1 * k slope regime (as opposed to 2 * k).
2. The momentary spring displacement is faster than the wave propagation to the opposing side. I.e. when the end-effector jerks to one side the opposing belt end hasn’t yet realized it and had a chance to relax.
3. There is another other (serial) spring in the system reducing the ringing frequency.

So let’s test these:

1. We can model our belt as a vibrating string. Plucking my belt between two idlers 417 mm apart gives a 65 Hz tone. The base frequency for a string is f₁ = sqrt(T/(m/L))/(2*L), T=tension (N), L = length, m = mass. The best value I found for the mass of a 2mm pitch 6mm wide GT3 belt is 7.8 g/m. Plugging these numbers in gives a tension of 26 N. Since this is substantially higher than the 5 N of acceleration force we can reject this hypothesis.

2. The wave propagation speed through a string is sqrt(T/(m/L)), or f₁ * 2L. 65 Hz * 2 * 0.417m = 54.2 m/s. My belt is ~1.4 m end-to-end, so it takes 26 ms for a wave to propagate through it. Since this is substantially longer than even the half-period of ringing (1/60 Hz) / 2 = 8.3 ms I think we have our answer. The opposing belt will not have had time to relax its counter force for more than a full period of the ringing leading to the lower slope characteristic of the spring function.

[DigitalVision]

@sebkritikel said in A Software Solution to Eliminate Ringing?:

@DigitalVision The X and U axis belts are each 1256mm in total length (GT2, 2mm pitch, 9mm width, through SDP/SI (GT3 was not available in that length at the time of purchasing)), so about 600mm center to center (motor to idler).

Interesting. Making a lot of assumptions (like the motor is to the right) and modeling the belt-spring characteristics gives:

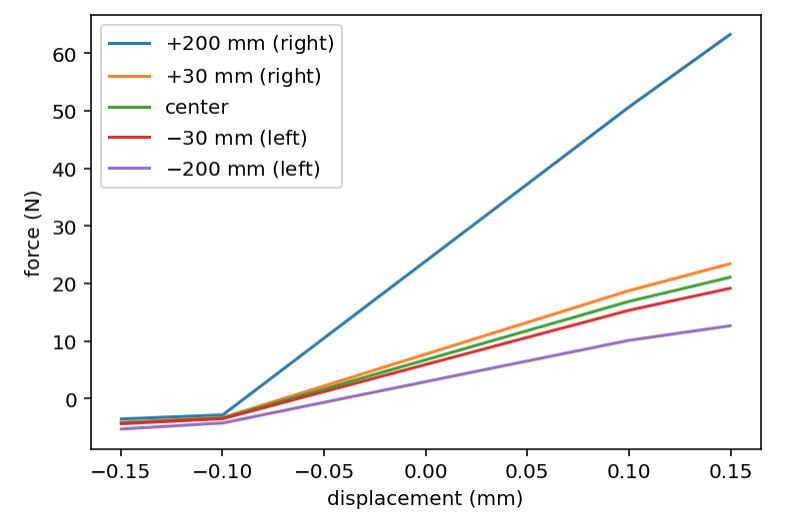
You can see how you get dramatically different spring "constants" (slopes) depending on the x position, with the position near the motor being substantially stiffer than positions further away.

Even across your 60 mm test print, you should see some 17 % higher x-spring constant on the right side than the left. This translates to an 8 % difference in f_n. I think it's clear that I need to augment the model with a position dependent parameter.

[DigitalVision]

@T3P3Tony said in A Software Solution to Eliminate Ringing?:

@DigitalVision
Really great work, and a nice overlap with some work I am doing looking at prints (although that is initially focused on pressure advance)

Thanks! Very interested to hear more about the pressure advance explorations.

Another effect we have seen probably relates to the forces acting on the extruder from the associated cable chains, wires etc, and how the change in different parts of the print area. Depending on how your machine is setup these can either have a large or almost negligible effect.

That's an interesting aspect I hadn't thought about in this context. I've certainly seen the cable bundle and/or bowden tube affecting e.g. delta bed leveling in the past.

[DigitalVision]

Update...

I was a bit concerned about the idea that wave propagation delay in the belts would be significant enough to affect the spring-damper model as my earlier calculation indicated. I'm happy to conclude that I was wrong. I had calculated the transversal wave propagation velocity when what actually matters is the longitudinal wave propagation velocity (or speed of sound) which is substantially higher. For my GT3 belt, the speed of sound is around 1.5 km/s which means that the force propagation delay over my longest belt segment is <1 ms. We need to make signal changes at close to kHz speeds for this to become relevant. I made a small simulation to convince myself of this, and as long as the belt tension is substantially higher than the maximum acceleration force the belt will behave as a perfect spring. Here’s a great source on theory of longitudinal wave propagation: https://www.mathpages.com/home/kmath569/kmath569.htm

The complication is that the spring "constant' is dependent on the spring length which changes with the position. Luckily we can measure and calculate this correction almost perfectly. Here’s a plot of how the ringing frequency theoretically changes across the print bed for a cartesian and CoreXY printer respectively. We can see how the two-belt CoreXY design balances the effect much better than a single linear-belt (with the stepper on one side) does. The linear belt design has a substantially higher spring stiffness when the print head is close to the stepper than when it’s far away and I think it’s clear that we need a positional parameter even for the CoreXY system.

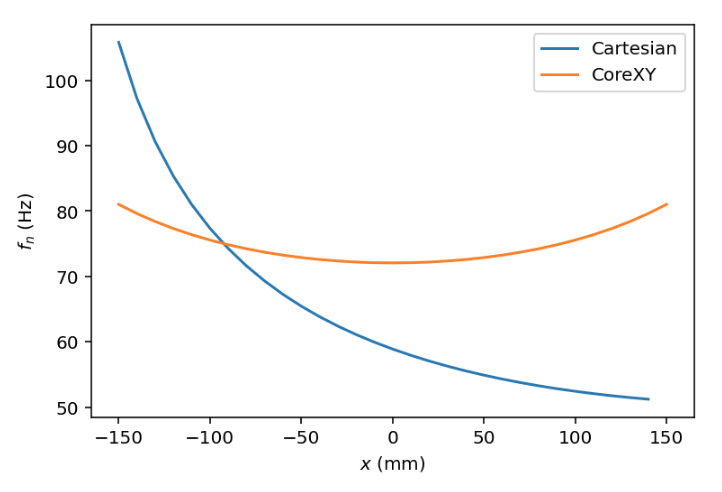
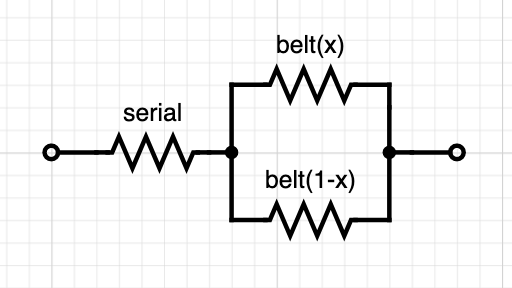
Both of these functions are of the form sqrt(1/p) where p is a quadratic polynomial. For the cartesian case p(x) has 3 parameters of which one is the relative belt lengths for a given x-coordinate and can be easily measured. If we add other serial springs to the system (like the stepper motors and compliant mechanics) we get another simple additive term. Measuring f_n at two different positions will determine the entire system.

For a CoreXY system it gets a bit more complicated since the belt lengths depend on both x and y. The compounded spring model is also a bit more complicated:

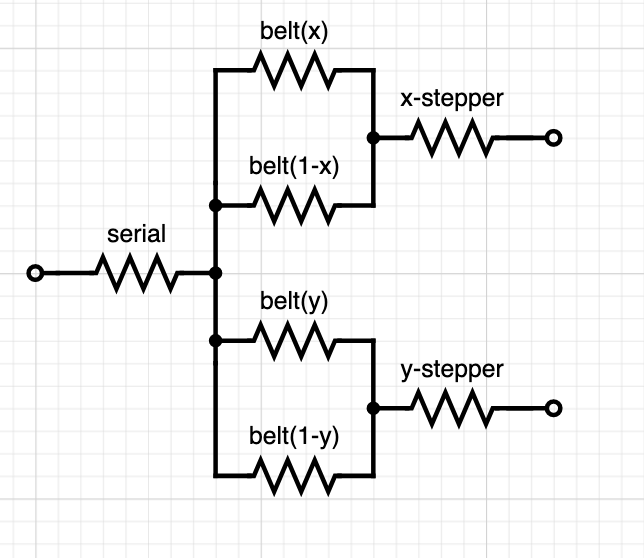
For one axis, we have 5 unknown parameters: stiffness of the x and y belt respectively, the serial spring at the end effector and the two stepper springs. We can probably assume that the two steppers are identical and collapse them to one parameter, but we are still left with 4 parameters. For the other axis, many of these parameters overlap. The steppers and belts are identical with only a difference in the driven mass. The serial spring is also different. So we have a total of 6 parameters across two axes. This means that we need to measure f_n for three points per axis rather than two to determine the parameters for the system.

One more thing. Can we calculate the spring constant from a stepper motor? The electrical field in the motor is effectively a spring, and at a static position the spring constant may at a first order be able to be calculated as the holding torque over one full step. I.e. once you exceed the holding torque the stepper will be closer to the next step 2 steps away than the current one and skip.

My stepper's data sheet claim a holding torque of 0.43 Nm and are rated at 1.684 A. I run them at 85% max current though, so 0.37 Nm. They have a 0.9° step size, 18 tooth pulleys with 2mm pitch belt, so the radius is 5.7 mm. If I calculate correctly, this gives me a spring constant of 710,000 N/m or around 10x higher stiffness than the belts. The impact is still a reduction of f_n of around ~4 Hz though, so not insignificant. I wonder if this linear spring force calculation is valid (especially for micro stepping too) though. There is definitely a reduction in torque at speed too. How significant is that at the speeds we run at?

[bot]

Thank you for the work you are putting into this.

Have you seen the variable ringing effects that change with the belt segment length, or is this just theory?

I have a cartesian printer, and would be interested in verifying whether the ringing is different if the toolhead is at different locations. Do you have any tests in mind that I could perform that would be helpful to show you?

I have a hope that you could be wrong about the variation. A guitar string has a fixed length by having two fixed points. The wave originates as a transverse wave from a plucked string.

On the other hand, a belt system has one fixed point: the motor pulley, with an idler. There is still tension beyond the idler. The wave from motion is more of a longitudinal wave, isn't it? So the idler doesn't exactly perfectly impede the wave. It might damp some of the transverse waves that may be induced, but the longitudinal wave seems like it would be able to "flow" right on past the idler, because the belt itself is what determines the position of the idler.

Again, I'm an idiot so I could be wrong and tell me if you think this is the case. But perhaps the variation of ringing won't be as severe as you imagine. I hope!

[DigitalVision]

Thanks for your input @bot!

Have you seen the variable ringing effects that change with the belt segment length, or is this just theory?

No, I've not seen it at all, so it's more of a hypothesis than theory at this point. Would love some help to test it though.

I have a cartesian printer, and would be interested in verifying whether the ringing is different if the toolhead is at different locations. Do you have any tests in mind that I could perform that would be helpful to show you?

That would be great! I'd simply print two hollow test cubes at two different positions on the bed. One close to the stepper, another one far away. Print at settings that excite ringing. Say ≥80mm/s, high acceleration (5000~10,000 mm/s) and compare the ringing frequency. If the model is true there should be a significant difference in ringing frequency at the two sides.

I have a hope that you could be wrong about the variation. A guitar string has a fixed length by having two fixed points. The wave originates as a transverse wave from a plucked string.

On the other hand, a belt system has one fixed point: the motor pulley, with an idler. There is still tension beyond the idler. The wave from motion is more of a longitudinal wave, isn't it? So the idler doesn't exactly perfectly impede the wave. It might dampen some of the transverse waves that may be induced, but the longitudinal wave seems like it would be able to "flow" right on past the idler, because the belt itself is what determines the position of the idler.

Interesting thought. If true, it would dramatically simplify things, although I don't think it's going to be true.
I don't consider the idler at all. I'd consider it as a very weak damper for longitudinal force propagation. The three points on the belt I consider are the two attachment points to the end effector and the motor pulley in between. We operate far below the propagation speed of the longitudinal wave, so I think we can think of the belts as operating in DC mode with the motor pulley applying a tension force on one belt segment and relaxing the force on the other segment. I.e. the only dynamic component that matters is the end effector's inertial movement.

Edit: Here's a quick sketch:

[bot]

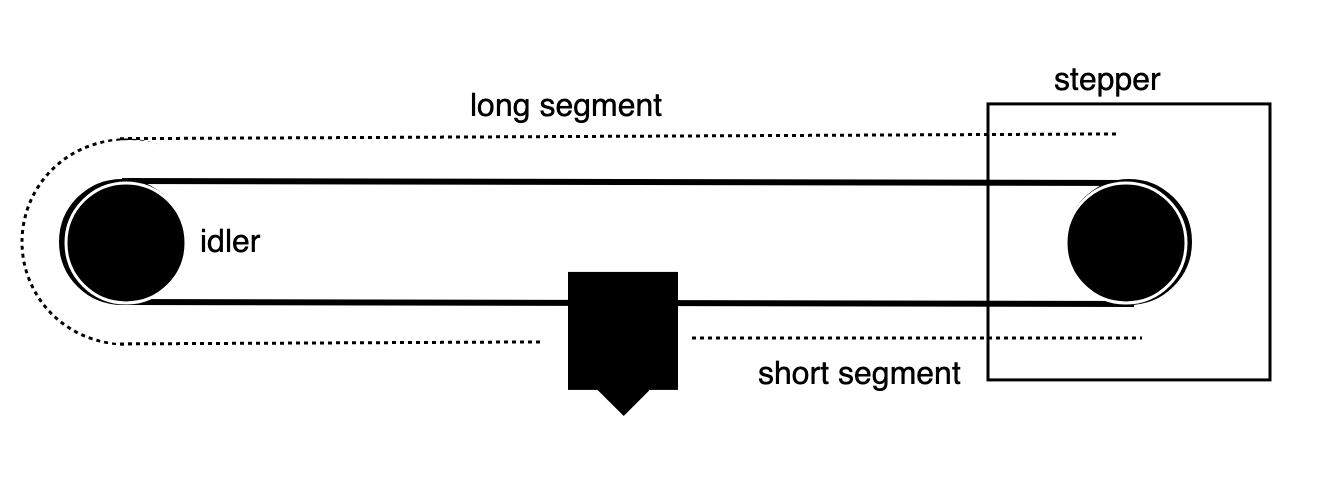
I also have a feeling you're right. I was just trying to come up with some way that it would be more simple! haha. I will perform some tests like you recommend.

Edit: @DigitalVision With your updated sketch, I understand more clearly how you are thinking of the system.

So if the "short segment" is as long as possible, that is the worst case scenario?

Edit 2: Now that I understand what you mean, and think about it a little bit, it seems obvious that what you are saying is likely true. I have about 8 hours of printing to do before I can do the tests but I will get to it as soon as possible.

[DigitalVision]

@bot

So if the "short segment" is as long as possible, that is the worst case scenario?

Correct. The belt segments get less compliant the shorter they are. If your belt's total length is 1, when you combine the two belt segments in parallel, the net compliance is proportional to x*(1-x). The maximum for this expression is at x=0.5 – i.e. the middle of the belt.

[bot]

I did some quick tests. This seems like evidence in support of your theory. I wasn't able to precisely measure the frequency differences, but there is clearly some differences in frequency happening.

Just FYI: I have a ridiculously long primary drive belt on my Y axis, which I think is causing havoc and also creating its own ringing that is interacting with the other ringing...

Nonetheless, this shows the front face, which is printed from top to bottom in this picture, along the X axis in a positive direction. One is printed "best case" for both axes, one is printed "worst case." The one on the right is "best case."

I had to increase my print acceleration from 1200 to 5000 to be able to see this large difference. My initial tests had much less ringing, and it appeared identical. I have to rule out that Y axis primary belt from the equation before this is useful.

It seems like a good strategy for the time being (for avoiding the effects of this variation) is to simply select an acceleration value that is low enough to not exhibit ringing to any discernible amount: this way, the variation is basically irrelevant. Do you think s-curve acceleration alone, before any cancellation of frequencies, would provide speed benefits in this regard? By this I mean, instead of trying to dynamically cancel out any ringing, by simply choosing conservative values that don't exhibit enough ringing to care about the variation: would S-curve help speed up the print in this case, while maintaining the "invisibility" of the ringing? Sorry if that question derails the topic too much for you.

[dc42]

S-curve acceleration reduces high frequency ringing, but the maths indicates that it actually increases ringing at some lower frequencies assuming you keep the total acceleration time constant. Whether a frequency counts as "low" or "high" depends on how its period compares to the total acceleration or deceleration time.

[bot]

@dc42 In my experience, it's easy to avoid the low-frequency ringing by choosing sensible acceleration/jerk/speed settings. It's the high-frequency ringing that is nearly impossible to be rid of. No matter how low of a jerk and accel/speed value I use, there is always a tiny amount of HF ringing.

Maybe I'm tuning things wrong, but I've been through basically the entire range of combinations and it reacts quite predictably.

I think, dc42, you've been right all along that the instantaneous speed change "problem" is the one to focus on first. The last bit of HF ringing I get seems related to jerk more than acceleration, and finding a low enough "jerk" speed for sharp corners while maintaining curve speed/quality is kind of impossible.

I don't mean to derail the thread. I'm very interested in the dynamic cancellation of ringing, if possible! But there is groundwork to be laid first, I think.

[DigitalVision]

@bot thanks for running this test. I must say it's hard to spot the ringing in the pictures. One thing I found useful was to limit the y axis acceleration to a very low value, say 500 while increasing x axis acceleration to a high value to avoid the cross talk. (Also make sure you've adjusted both M204 and M201).

It seems like a good strategy for the time being (for avoiding the effects of this variation) is to simply select an acceleration value that is low enough to not exhibit ringing to any discernible amount: this way, the variation is basically irrelevant.

The ringing magnitude is proportional to the acceleration so while you can mitigate it with lower acceleration settings it has the potential to affect the print time significantly, especially on print geometries with shorter path lengths. An illustration of print speed vs acceleration for different segment lengths.

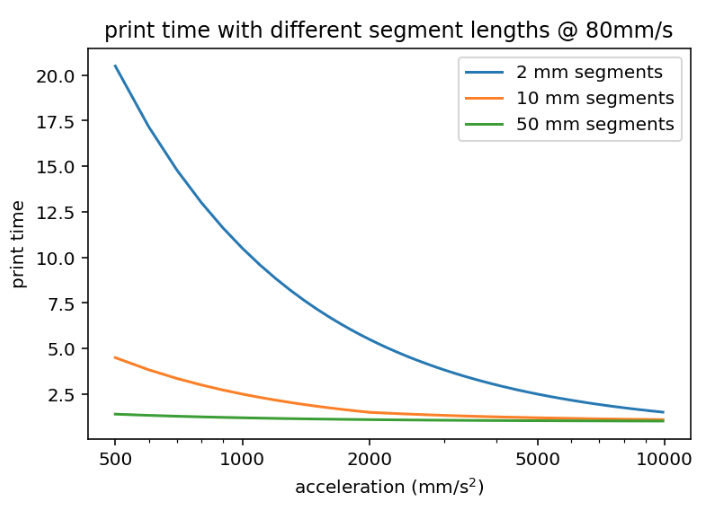
Do you think s-curve acceleration alone, before any cancellation of frequencies, would provide speed benefits in this regard?

In addition to what dc42 said – the photo at the very top of this topic shows an s-curve vs linear acceleration ramp profile without any appreciable difference in ringing.

[bot]

So it's safe to say we can rule out S-curve as beneficial? Or it is only beneficial with your modelling implementation?

I definitely understand the print time implications of acceleration, and will support any and all theories which can improve print time while maintaining or improving quality.

I have highlighted the photo to better show what I think are signs of ringing. By my eye it's easier to see and tell that they are at least different, which supports your theory.

[DigitalVision]

@bot said in A Software Solution to Eliminate Ringing?:

I think, dc42, you've been right all along that the instantaneous speed change "problem" is the one to focus on first. The last bit of HF ringing I get seems related to jerk more than acceleration, and finding a low enough "jerk" speed for sharp corners while maintaining curve speed/quality is kind of impossible.

I personally don't think the implementation of "jerk"/instantaneous speed change as implemented in all current firmwares is very good. The purpose of jerk is to allow continuous speed through linearly segmented curves, but as a consequence you get abrupt changes (and ringing) for sharp corners too. A quick thing I don't know has been tested and I would expect to be a better heuristic would be to add a corner angle threshold and disable jerk for any corner beyond a certain angle. This is quite often used in 3D graphics as a heuristic to for when to smooth vs flat shade a 3d mesh and seems to work fairly well. You may want to mix in segment length as well in a heuristic, but in either case it shouldn't be hard to prevent "jerk" from applying to a 90° corner between two long segments.

[DigitalVision]

@bot said in A Software Solution to Eliminate Ringing?:

So it's safe to say we can rule out S-curve as beneficial? Or it is only beneficial with your modelling implementation?

I'd be surprised if s-curves by themselves allow you to increase the print speed, but they will eliminate the HF transients at the ends of ramps. The trade-off is that they lead to higher peak accelerations if you want to preserve the same print time, and that means that you load the "spring" more. But s-curves allows the spring compensation model to work without requiring instantaneous position changes. And I've found this allows for substantially higher accelerations.

I have highlighted the photo to better show what I think are signs of ringing. By my eye it's easier to see and tell that they are at least different, which supports your theory.

Thanks, those lines help! Could you give a rough estimate of the short and long belt length for the two print locations?

[bot]

@DigitalVision Sure the belt lengths are like this:

It's a 50 mm edge length on that print

X axis "best case"
Short length: 166 mm to 216 mm
Long length: 970 mm to 920 mm

X axis "worst case"
Short length: 366 mm to 416 mm
Long length: 770 mm to 720 mm

Y axis numbers are similar.

[DigitalVision]

@bot said in A Software Solution to Eliminate Ringing?:

Short length: 166 mm to 216 mm
Long length: 970 mm to 920 mm
X axis "worst case"
Short length: 366 mm to 416 mm
Long length: 770 mm to 720 mm

Cool. Your "best" case should have up to 75 % higher spring constant than the worst side (very dependent on which side of the print was at the most extreme point). If your belts dominate ringing, this should translate into ~32% higher ringing frequency, so the good side ringing period should be as little as ~3/4 of the worse side (with the stepper motor and other serial springs the difference will be slightly smaller though). That seems possible from your photo.

I don't know what that secondary ringing at around 2/3s of the print is though. That far too early to be at the deceleration ramp but also too late to be a late residual from the earlier corner.

[bot]

@DigitalVision I think it's best not to look to deeply into my tests. I didn't isolate the Y axis as you mentioned, and my Y axis is insanely stupid to begin with (there is a longer "short side" on the primary drive than at any point of the secondary drive belt. I don't know what I was thinking at the time). I have plans to change it to be "the same" as the X axis, just with more weight to move around. Then I will perform more tests.

All I wanted to do was confirm or deny the idea that the ringing was variable (in frequency) depending on where it was printed. I feel like I confirmed that and your theories all seem to line up.

So, given all that, would using your method be as simple as determining the different frequencies at different parts of the axes, and cancelling as required based on position?

[DigitalVision]

@bot said in A Software Solution to Eliminate Ringing?:

So, given all that, would using your method be as simple as determining the different frequencies at different parts of the axes, and cancelling as required based on position?

Yes, in theory at least. For a cartesian all you would need is to determine the frequencies at two different positions per axis and provide the positive and negative belt lengths at a known location. One could probably create a nice script to automatically generate the right structures to print at the known locations. I found it most easy and consistent to spot the acceleration ringing (where the extrusion width oscillates), and especially when printing in a semi-translucent material. Here's a photo on silver filament which is very hard to capture on photo showing the phase inversion in the ringing pattern as the f_n parameter was varied across the print z. If you get it right, there is a rather sharp region without ringing that's fairly easy to spot and measure:

[bot]

@DigitalVision The results are truly fantastic.

Do you think it would be easier or harder to determine the "positional frequency" on a corexy machine? A delta?