Maximum Acceleration Calculator

sebkritikel

@genewild said in Maximum Acceleration Calculator:

Hi! Thanks for making this tool, it is very handy.

I'm currently trying to grasp the limitation of accelleration on stepper motor drives. I've used your calculator on a few motors, and i noticed that generally people report running 2-4 times higher accelleration on their printers before running into issues than your calculator says is possible.

I am not sure these printers actually run at the requested speed, but certainly there is some difference between running at the speed your calculator produces and a vastly higher speed, i can see that on my own printer which accellerates more violently.

So i am wondering, what gives? Shouldn't the stepper skip steps if you ask it to go TOO fast? The stepper driver has no feedback loop to tell. I can't notice lost steps below 20.000 mm/s² accelleration using really small NEMA 17 motors with only 1.68 A capability and a rated torque of only 36Ncm, inertia of 54 g/cm² driving a rather heavy gantry at 800gr.

I would really apprechiate if someone could explain this discrepancy to me, i am not very familiar with stepper drives.

You raise some good questions - and unfortunately I'm not the one that can appropriately answer them.

I too see a lot of discussions of folks using acceleration values ~10x what I would expect. A related reason why this and the inverse is true (why the calculator is 10% of what some other folks are using) is because of the below fact:

https://forum.duet3d.com/topic/6/stepper-motors-for-corexy
From: @dc42

If you want the motion lag to be no more than one 1/16 microstep during acceleration, then you need to multiply by 9.8%. So the available torque is 65 * 0,85 * 0.71 * 0.098 = 3.8Ncm.

In the past the general consensus was to multiply by the available torque for a given stepper by 9.8% as a sort of factor-of-safety. I follow this factor-of-safety approach.

I recently came across this super cool spreadsheet - however the equations/macros omits the factor-of-safety for available torque, while using it when calculating what the required torque is - the opposite of what I would expect. Here is an example screen grab of a few motors using the equations (without the factor-of-safety):

The chart shows the expected speeds at which motor torque begins to drop off - which match the Duet calculations for max speeds here:
https://duet3d.dozuki.com/Wiki/Choosing_and_connecting_stepper_motors

The issue, to me, is that the red dashed line for torque required is of an extraordinarily low value relative to the stepper curve maximums. A (in my eyes, appropriately allocating the factor-of-safety) corrected chart is below - note the Y-axis changes:

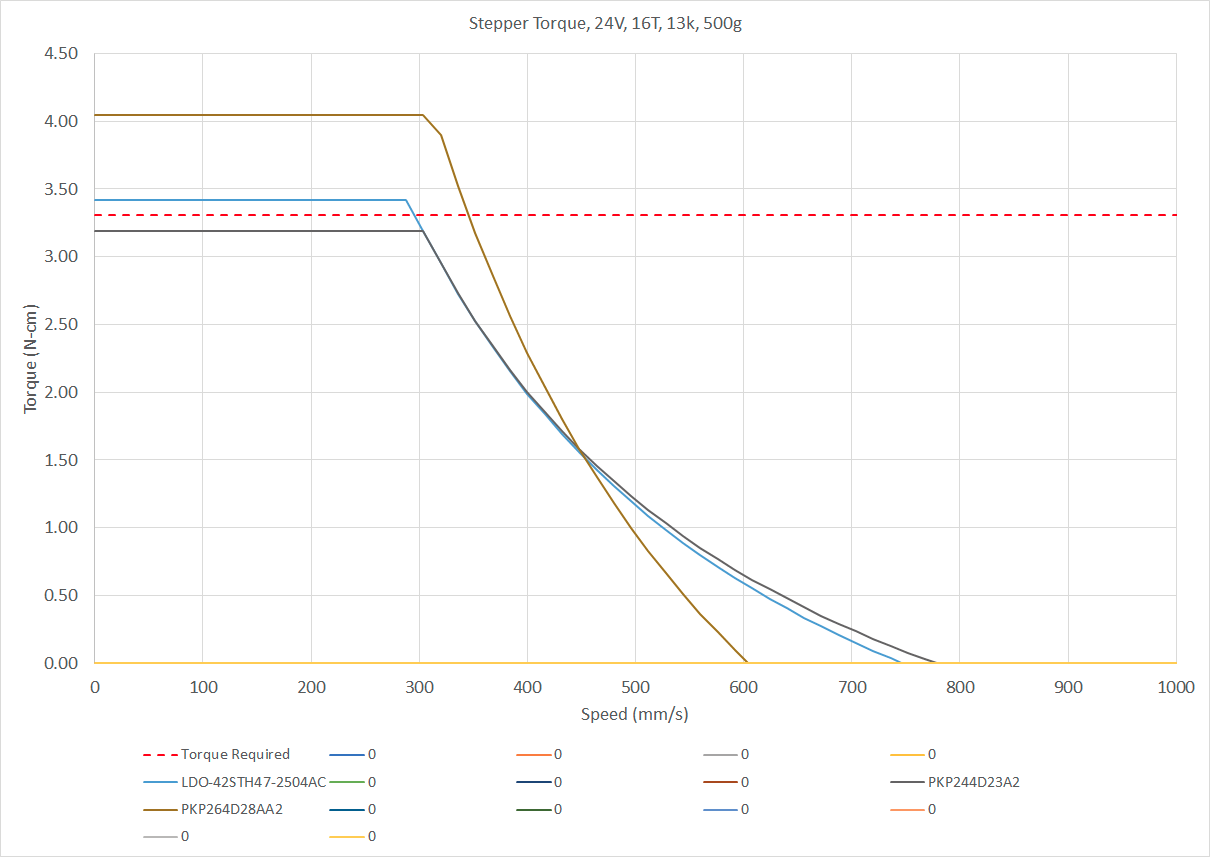
Anyways, more to dig in there. Perhaps @dc42 can go into more detail regarding the motion lag considerations at 1/16th of a microstep. Maybe nowadays that consideration isn't too big of a deal.

Side note - but most folks I see using more than, say, 20,000 mm/s^2 acceleration values (on motor/machine setups I would calculate having issues) typically run Klipper. Perhaps issues they may see at such accelerations are reduced by that input-shaping implementation.

Tinchus

Hi all. Question: the calculator here https://wilriker.github.io/maximum-acceleration-calculator/ request some data but what is about the case where you dont use pulleys? (axis moved directly using ballscrews for example)

wilriker

@Tinchus said in Maximum Acceleration Calculator:

Hi all. Question: the calculator here https://wilriker.github.io/maximum-acceleration-calculator/ request some data but what is about the case where you dont use pulleys? (axis moved directly using ballscrews for example)

In case of using any kind of screw to directly drive the axis you can approximate the pulley radius by dividing the screw lead by 2π. Remember to before or after convert from whatever unit you used to centimeters (if necessary). The value will probably be a tad bit too large but not in the amount that matters - and you should anyways always remove a security margin.

Example
if your screw has a lead of 2mm, i.e. every full rotation results in movement of 2mm, then you divide

2mm/2π=0.31831mm

Divide that again by 10 to convert it into cm and you have your virtual pulley radius.